Предмет: Математика,
автор: foreverksusha1
Помогите решить систему уравнений, пожалуйста
Приложения:
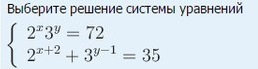
Ответы
Автор ответа:
1
Получится вот так :)
Приложения:

Автор ответа:
1
Пусть
Похожие вопросы
Предмет: Другие предметы,
автор: MARGO2109
Предмет: Қазақ тiлi,
автор: Аноним
Предмет: Русский язык,
автор: mmm2puhgyhg
Предмет: Английский язык,
автор: dasha9529
Предмет: Математика,
автор: kolanmackovskij615