Предмет: Математика,
автор: yulia199829
В прямоугольном треугольнике угол между высотой и медианой ,проведёнными из вершины прямого угла ,равен 20 градусов .Найдите больший из острых углов этого треугольника .
Ответы
Автор ответа:
2
Из подобия треугольников АВС и НСВ следует, что ∠ В=∠НСА.
Медиана, проведенная из вершины прямого угла, равна половине гипотенузе. Значит треугольник МВС – равнобедренный, и ∠ВСН=∠В=∠НСА.
∠НСА+∠ВСН=90°–∠МСН=90 °–20 °=70°; ∠НСА=70:2=35°.
∠А=90°–∠НСА=90°–35°=55°.
ОТВЕТ: 55°
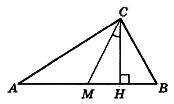
рисунок смотри на фото
Медиана, проведенная из вершины прямого угла, равна половине гипотенузе. Значит треугольник МВС – равнобедренный, и ∠ВСН=∠В=∠НСА.
∠НСА+∠ВСН=90°–∠МСН=90 °–20 °=70°; ∠НСА=70:2=35°.
∠А=90°–∠НСА=90°–35°=55°.
ОТВЕТ: 55°
рисунок смотри на фото
Приложения:
Похожие вопросы
Предмет: Английский язык,
автор: cool109
Предмет: Английский язык,
автор: samir1212
Предмет: Русский язык,
автор: Cwitd
Предмет: Математика,
автор: dariasp861
Предмет: Математика,
автор: 2012ocen