Предмет: Алгебра,
автор: Аноним
Помогите с подробным решением пожалуйста Ответы 1) (7;5]
2)y=x-6
Приложения:

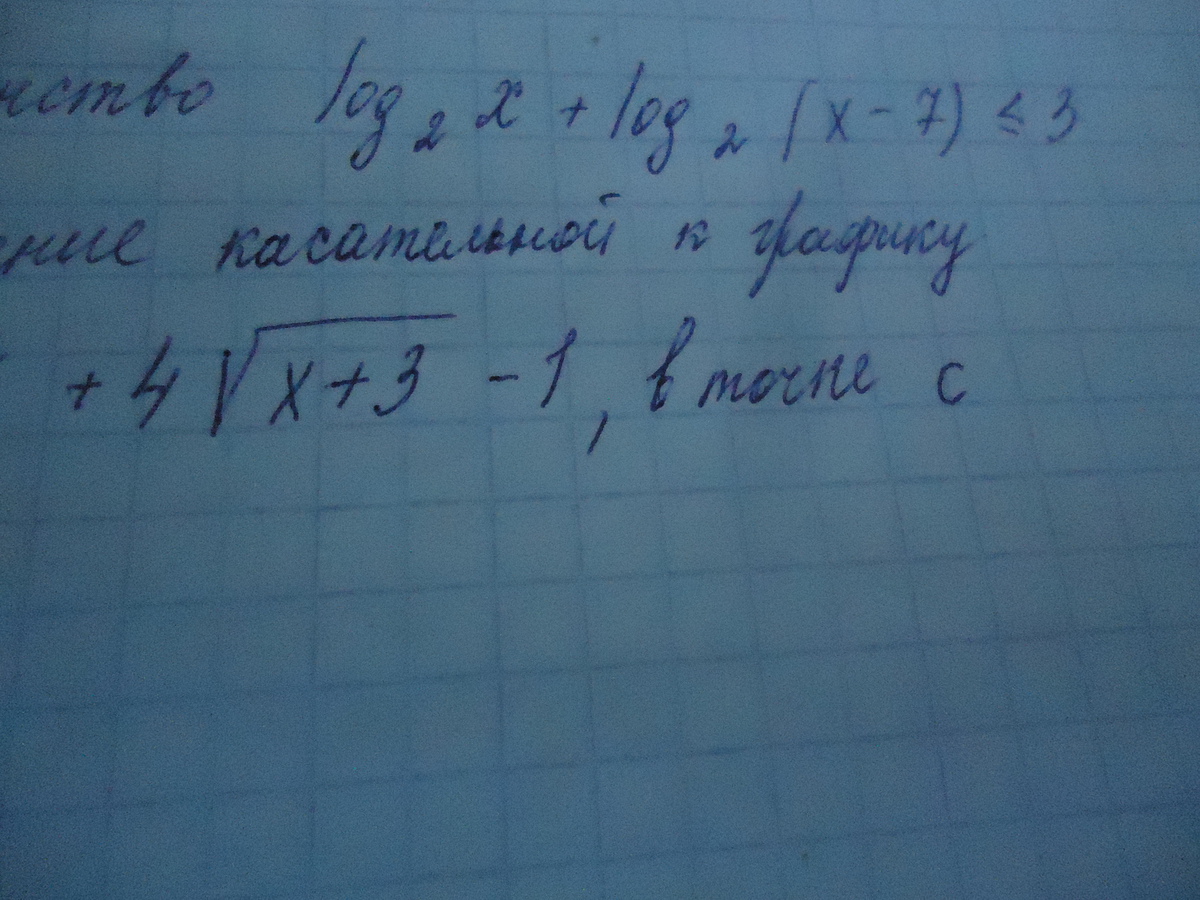
Ответы
Автор ответа:
0
1) Loq(2) x +Loq(2) (x -7) ≤ 3 ; * * * ОДЗ: { x >0 ; x -7 >0⇒ x >7. * * *
{ x >0 ; x -7 >0 ; Loq(2) x(x -7) ≤ Loq(2) 2³.
{x >7 ; x(x -7) ≤8 . {x >7 ; x² -7x -8 ≤ 0 . {x >7 ; (x+1)(x-8) ≤ 0 .
{x >7 ; - 1 ≤ x ≤ 8⇔ 7 <x ≤ 8 .
ответ : x ∈(7; 8] .
2) f(x) =e^(2x-2) +4√(x+3) -1 , x₁ =1.
---------------------------------------------
Уравнение касательной к графику функции f(x) в точке x₁ имеет вид :
y - f (x₁) = f '(x₁)*(x-x₁) (1) ;
f (x₁) = f (1) =e^(2*1-2) +4*√(1+3) -1 = e^0 +4*2 -1 =1+8 -1 = 8 ;
f '(x) =(e^(2x-2) +4√(x+3) -1)' =(e^(2x-2))' +(4√(x+3))' -1' =e^(2x-2)*(2x-2)' +4*1/(2√(x+3)) +0=
=2*e^(2x-2) +2/√(x+3);
f '(x₁) = f '(1) =2e^(2*1-2) +2/√(1+3) =2*e^0 +2/2 =2*1 +1 =3;
найденные значении поставим в (1) получим :
y - 8 = 3(x-1) ;
y = 3x +5 .
{ x >0 ; x -7 >0 ; Loq(2) x(x -7) ≤ Loq(2) 2³.
{x >7 ; x(x -7) ≤8 . {x >7 ; x² -7x -8 ≤ 0 . {x >7 ; (x+1)(x-8) ≤ 0 .
{x >7 ; - 1 ≤ x ≤ 8⇔ 7 <x ≤ 8 .
ответ : x ∈(7; 8] .
2) f(x) =e^(2x-2) +4√(x+3) -1 , x₁ =1.
---------------------------------------------
Уравнение касательной к графику функции f(x) в точке x₁ имеет вид :
y - f (x₁) = f '(x₁)*(x-x₁) (1) ;
f (x₁) = f (1) =e^(2*1-2) +4*√(1+3) -1 = e^0 +4*2 -1 =1+8 -1 = 8 ;
f '(x) =(e^(2x-2) +4√(x+3) -1)' =(e^(2x-2))' +(4√(x+3))' -1' =e^(2x-2)*(2x-2)' +4*1/(2√(x+3)) +0=
=2*e^(2x-2) +2/√(x+3);
f '(x₁) = f '(1) =2e^(2*1-2) +2/√(1+3) =2*e^0 +2/2 =2*1 +1 =3;
найденные значении поставим в (1) получим :
y - 8 = 3(x-1) ;
y = 3x +5 .
Похожие вопросы
Предмет: Другие предметы,
автор: nikolay2006bart
Предмет: Русский язык,
автор: ааааавввв
Предмет: Русский язык,
автор: рустам222
Предмет: Алгебра,
автор: Амир43124
Предмет: Математика,
автор: anna7777717