Предмет: Алгебра,
автор: utilinaa
Помогите решить 15 номер, пожалуйста. ❤️❤️❤️
Приложения:
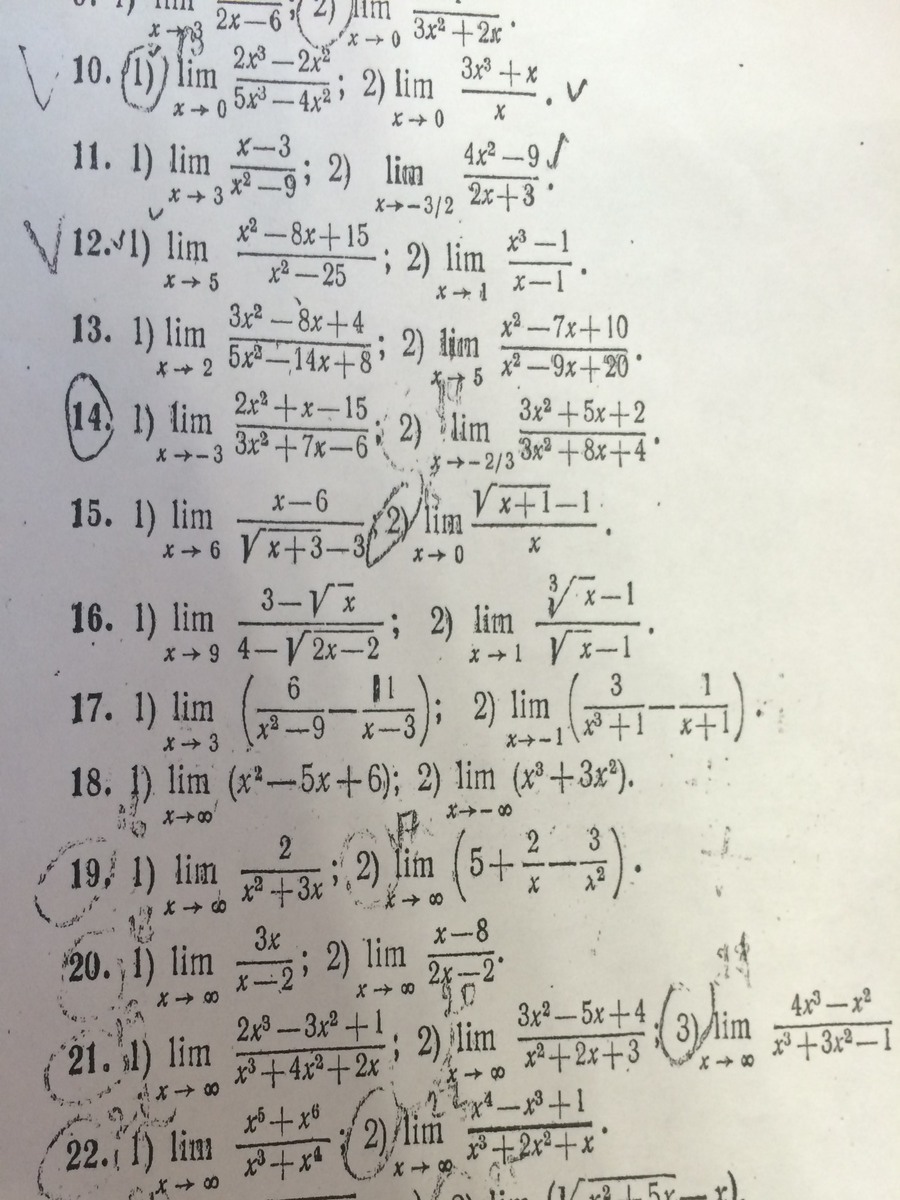
Exponena:
а по Лопиталю никак?
Это как? Я просто проболела во время пределов, сейчас сама разбираюсь сижу
предел отношения функций равен пределу отношения их производных
Ответы
Автор ответа:
1
Спасибо огромное☺️☺️
Автор ответа:
1
Лопиталь
Спасибо☺️ теперь поняла вроде)
Похожие вопросы
Предмет: Русский язык,
автор: madina2503
Предмет: Қазақ тiлi,
автор: вовлвлвл
Предмет: Русский язык,
автор: milzinurowaoxrixg
Предмет: Русский язык,
автор: jahongir1383
Предмет: Физика,
автор: AreldBro