Предмет: Геометрия,
автор: kvast
Угол между высотами параллелограмма, проведенными с вершины тупого угла, равен 30 градусов. Найдите площадь параллелограмма, если его высоты равны 6 см и 16 см.
Ответы
Автор ответа:
50
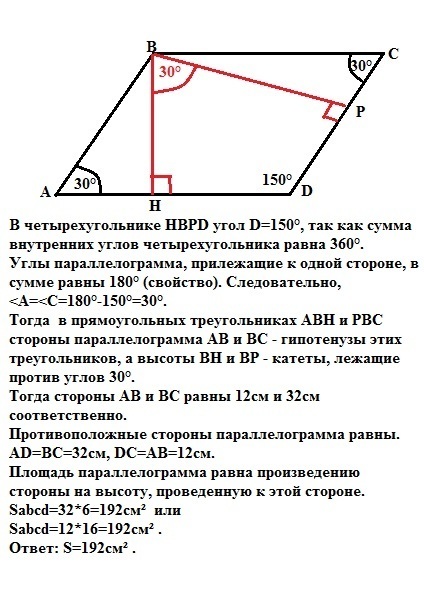
В четырехугольнике НВРD угол D=150°, так как сумма внутренних углов четырехугольника равна 360°.
Углы параллелограмма, прилежащие к одной стороне, в сумме равны 180° (свойство). Следовательно,
<A=<C=180°-150°=30°.
Тогда в прямоугольных треугольниках АВН и РВС стороны параллелограмма АВ и ВС - гипотенузы этих треугольников, а высоты ВН и ВР - катеты, лежащие против углов 30°.
Тогда стороны АВ и ВС равны 12см и 32см соответственно.
Противоположные стороны параллелограмма равны.
AD=ВС=32cм, DC=АВ=12см.
Площадь параллелограмма равна произведению стороны на высоту, проведенную к этой стороне.
Sabcd=32*6=192cм² или
Sabcd=12*16=192cм² .
Ответ: S=192см² .
Углы параллелограмма, прилежащие к одной стороне, в сумме равны 180° (свойство). Следовательно,
<A=<C=180°-150°=30°.
Тогда в прямоугольных треугольниках АВН и РВС стороны параллелограмма АВ и ВС - гипотенузы этих треугольников, а высоты ВН и ВР - катеты, лежащие против углов 30°.
Тогда стороны АВ и ВС равны 12см и 32см соответственно.
Противоположные стороны параллелограмма равны.
AD=ВС=32cм, DC=АВ=12см.
Площадь параллелограмма равна произведению стороны на высоту, проведенную к этой стороне.
Sabcd=32*6=192cм² или
Sabcd=12*16=192cм² .
Ответ: S=192см² .
Приложения:
Похожие вопросы
Предмет: Русский язык,
автор: hadija1908
Предмет: Окружающий мир,
автор: Melisaoz07
Предмет: Английский язык,
автор: snegincairina
Предмет: Русский язык,
автор: rabit17