Предмет: Алгебра,
автор: likusa11
Найти значение производной функции
Приложения:
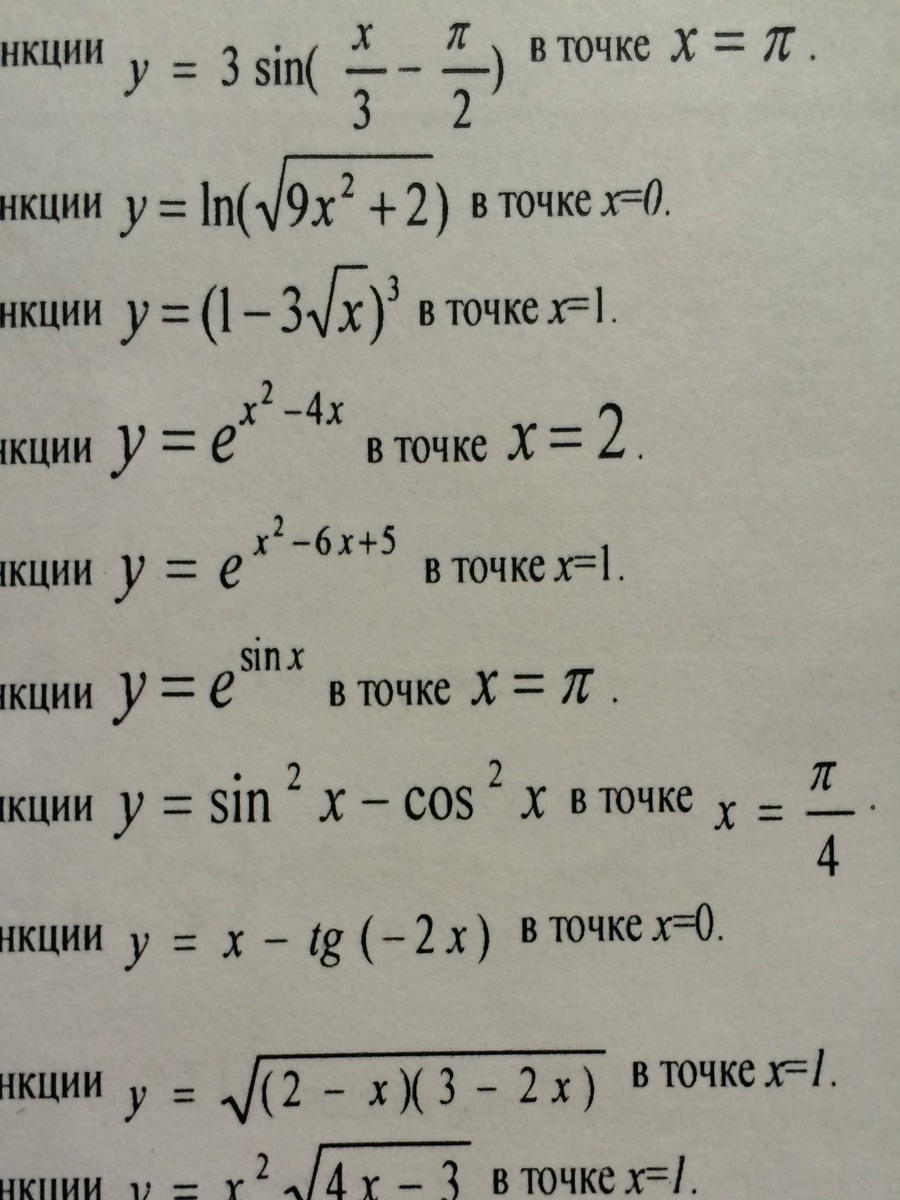
Ответы
Автор ответа:
1
1) y=3sin(x/3 - π/2)
y' = 3 * (1/3) cos(x/3 - π/2) =cos(x/3 - π/2)
При х=π y' = cos(π/3 - π/2) = cos (-π/6)=cos(π/6)=√3
2
2) y=ln √(9x² +2)
y' = 1 * 1 * 18x = 9x
√(9x²+2) 2√(9x²+2) 9x² +2
При x=0 y' = 9*0 = 0
9*0²+2
3) y=(1 - 3√x)³
y' = 3(1 - 3√x)² * -3 = -9(1-3√x)²
2√x 2√x
При х=1 у' = -9(1-3√1)² = -9 * 2 = -18
2√1
4) y=e^(x² -4x)
y' =(2x-4)e^(x² -4x)
При х=2 y' = (2*2-4)e^(2² -4*2)=0
5) y=e^(x²-6x+5)
y' =(2x-6)e^(x²-6x+5)
При х=1 y' =(2*1-6)e^(1-6+5)=-3e⁰=-3
6) y=e^(sinx)
y' = cosx * e^(sinx)
При х=π y' = cosπ * e^(sinπ)=-1*e⁰=-1
7) y=sin²x - cos²x = -(cos²x - sin²x)=-cos2x
y' = 2sin2x
При х=π/4 y' =2sin(2*(π/4))=2sin(π/2)=2
8) y=x - tg(-2x)=x +tg2x
y' = 1 + 2
cos²x
При х=0 y' = 1 + 2 = 1 +2 =3
cos² 0
9) y=√[(2-x)(3-2x)] =√(6-3x-4x+2x²) =√(2x²-7x+6)
y' = 4x-7
2√(2x² -7x+6)
При х=1 y' = 4-7 = -3 = -1.5
2√(2-7+6) 2
10) y=x² √(4x-3)=√[x⁴(4x-3)]=√(4x⁵ -3x⁴)
y' = 20x⁴ - 12x³ = 2x³(10x - 6) = x(10x-6)
2√(4x⁵ -3x⁴) 2x²√(4x-3) √(4x-3)
При х=1 y' = 1*(10-6) = 4
√(4-3)
y' = 3 * (1/3) cos(x/3 - π/2) =cos(x/3 - π/2)
При х=π y' = cos(π/3 - π/2) = cos (-π/6)=cos(π/6)=√3
2
2) y=ln √(9x² +2)
y' = 1 * 1 * 18x = 9x
√(9x²+2) 2√(9x²+2) 9x² +2
При x=0 y' = 9*0 = 0
9*0²+2
3) y=(1 - 3√x)³
y' = 3(1 - 3√x)² * -3 = -9(1-3√x)²
2√x 2√x
При х=1 у' = -9(1-3√1)² = -9 * 2 = -18
2√1
4) y=e^(x² -4x)
y' =(2x-4)e^(x² -4x)
При х=2 y' = (2*2-4)e^(2² -4*2)=0
5) y=e^(x²-6x+5)
y' =(2x-6)e^(x²-6x+5)
При х=1 y' =(2*1-6)e^(1-6+5)=-3e⁰=-3
6) y=e^(sinx)
y' = cosx * e^(sinx)
При х=π y' = cosπ * e^(sinπ)=-1*e⁰=-1
7) y=sin²x - cos²x = -(cos²x - sin²x)=-cos2x
y' = 2sin2x
При х=π/4 y' =2sin(2*(π/4))=2sin(π/2)=2
8) y=x - tg(-2x)=x +tg2x
y' = 1 + 2
cos²x
При х=0 y' = 1 + 2 = 1 +2 =3
cos² 0
9) y=√[(2-x)(3-2x)] =√(6-3x-4x+2x²) =√(2x²-7x+6)
y' = 4x-7
2√(2x² -7x+6)
При х=1 y' = 4-7 = -3 = -1.5
2√(2-7+6) 2
10) y=x² √(4x-3)=√[x⁴(4x-3)]=√(4x⁵ -3x⁴)
y' = 20x⁴ - 12x³ = 2x³(10x - 6) = x(10x-6)
2√(4x⁵ -3x⁴) 2x²√(4x-3) √(4x-3)
При х=1 y' = 1*(10-6) = 4
√(4-3)
likusa11:
спасибо большое)) а можете еще пару заданий решить , у меня экзамен завтра в колледже
нет
Похожие вопросы
Предмет: Русский язык,
автор: sabi0000
Предмет: Английский язык,
автор: MaksimIvanov32
Предмет: Русский язык,
автор: sabi0000
Предмет: Физика,
автор: JotaRumex
Предмет: Алгебра,
автор: napops00