Предмет: Математика,
автор: lenashnarr97
Помогите , пожалуйста!
Приложения:
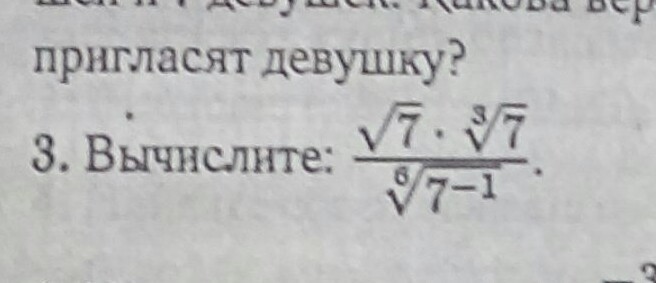
Ответы
Автор ответа:
1
Корень - это один из способов записи дробных показателей степени. Так что мы можем записать корни чисел в выражении в виде степеней этих чисел. Квадратному корню будет соответствовать степень 1/2, корню третьей степени - степень 1/3 и т.д.
![\frac{ \sqrt{7} * \sqrt[3]{7} }{ \sqrt[6]{ 7^{-1} } } = \frac{ 7^{ \frac{1}{2} }* 7^{ \frac{1}{3} } }{ ( 7^{-1} )^{ \frac{1}{6} } } \frac{ \sqrt{7} * \sqrt[3]{7} }{ \sqrt[6]{ 7^{-1} } } = \frac{ 7^{ \frac{1}{2} }* 7^{ \frac{1}{3} } }{ ( 7^{-1} )^{ \frac{1}{6} } }](https://tex.z-dn.net/?f=+%5Cfrac%7B+%5Csqrt%7B7%7D+%2A+%5Csqrt%5B3%5D%7B7%7D+%7D%7B+%5Csqrt%5B6%5D%7B+7%5E%7B-1%7D+%7D+%7D+%3D+%5Cfrac%7B+7%5E%7B+%5Cfrac%7B1%7D%7B2%7D+%7D%2A+7%5E%7B+%5Cfrac%7B1%7D%7B3%7D+%7D+%7D%7B+%28+7%5E%7B-1%7D+%29%5E%7B+%5Cfrac%7B1%7D%7B6%7D+%7D+%7D+)
Далее мы будем пользоваться свойствами степеней.
При возведении степени в степень показатели степени перемножаются между собой.
При умножении степеней с одинаковыми основаниями показатели степени складываются,

а при делении - вычитаются.

Любое число в первой степени равно самому себе: 7¹=7.
Вот так будет записан ход решения полностью:
![\frac{ \sqrt{7} * \sqrt[3]{7} }{ \sqrt[6]{ 7^{-1} } } = \frac{ 7^{ \frac{1}{2} }* 7^{ \frac{1}{3} } }{ ( 7^{-1} )^{ \frac{1}{6} } } = \frac{7 ^{ \frac{1}{2}+ \frac{1}{3} } }{ 7^{(-1)* \frac{1}{6} } } = \frac{ 7^{ \frac{3}{6}+ \frac{2}{6} } }{ 7^{- \frac{1}{6} } } = \frac{ 7^{ \frac{5}{6} } }{ 7^{- \frac{1}{6} } } = 7^{ \frac{5}{6} -(- \frac{1}{6} )} = 7^{ \frac{5}{6}+ \frac{1}{6} } = 7^{ \frac{6}{6} } = \\ = 7^{1} =7 \frac{ \sqrt{7} * \sqrt[3]{7} }{ \sqrt[6]{ 7^{-1} } } = \frac{ 7^{ \frac{1}{2} }* 7^{ \frac{1}{3} } }{ ( 7^{-1} )^{ \frac{1}{6} } } = \frac{7 ^{ \frac{1}{2}+ \frac{1}{3} } }{ 7^{(-1)* \frac{1}{6} } } = \frac{ 7^{ \frac{3}{6}+ \frac{2}{6} } }{ 7^{- \frac{1}{6} } } = \frac{ 7^{ \frac{5}{6} } }{ 7^{- \frac{1}{6} } } = 7^{ \frac{5}{6} -(- \frac{1}{6} )} = 7^{ \frac{5}{6}+ \frac{1}{6} } = 7^{ \frac{6}{6} } = \\ = 7^{1} =7](https://tex.z-dn.net/?f=+%5Cfrac%7B+%5Csqrt%7B7%7D+%2A+%5Csqrt%5B3%5D%7B7%7D+%7D%7B+%5Csqrt%5B6%5D%7B+7%5E%7B-1%7D+%7D+%7D+%3D+%5Cfrac%7B+7%5E%7B+%5Cfrac%7B1%7D%7B2%7D+%7D%2A+7%5E%7B+%5Cfrac%7B1%7D%7B3%7D+%7D++%7D%7B+%28+7%5E%7B-1%7D+%29%5E%7B+%5Cfrac%7B1%7D%7B6%7D+%7D+%7D+%3D+%5Cfrac%7B7+%5E%7B+%5Cfrac%7B1%7D%7B2%7D%2B+%5Cfrac%7B1%7D%7B3%7D++%7D+%7D%7B+7%5E%7B%28-1%29%2A+%5Cfrac%7B1%7D%7B6%7D+%7D+%7D+%3D+%5Cfrac%7B+7%5E%7B+%5Cfrac%7B3%7D%7B6%7D%2B+%5Cfrac%7B2%7D%7B6%7D++%7D+%7D%7B+7%5E%7B-+%5Cfrac%7B1%7D%7B6%7D+%7D+%7D+%3D+%5Cfrac%7B+7%5E%7B+%5Cfrac%7B5%7D%7B6%7D+%7D+%7D%7B+7%5E%7B-+%5Cfrac%7B1%7D%7B6%7D+%7D+%7D+%3D+7%5E%7B+%5Cfrac%7B5%7D%7B6%7D+-%28-+%5Cfrac%7B1%7D%7B6%7D+%29%7D+%3D+7%5E%7B+%5Cfrac%7B5%7D%7B6%7D%2B+%5Cfrac%7B1%7D%7B6%7D++%7D+%3D+7%5E%7B+%5Cfrac%7B6%7D%7B6%7D+%7D+%3D+%5C%5C+%3D+7%5E%7B1%7D+%3D7)
Далее мы будем пользоваться свойствами степеней.
При возведении степени в степень показатели степени перемножаются между собой.
При умножении степеней с одинаковыми основаниями показатели степени складываются,
а при делении - вычитаются.
Любое число в первой степени равно самому себе: 7¹=7.
Вот так будет записан ход решения полностью:
Похожие вопросы
Предмет: Русский язык,
автор: annaosheiko
Предмет: Английский язык,
автор: родион86
Предмет: Қазақ тiлi,
автор: amina113
Предмет: Математика,
автор: exclu74
Предмет: Физика,
автор: Egorka123654