Предмет: Геометрия,
автор: Ho1ho2ho3
Срочно! Потом отдам много баллов
Приложения:
Ответы
Автор ответа:
0
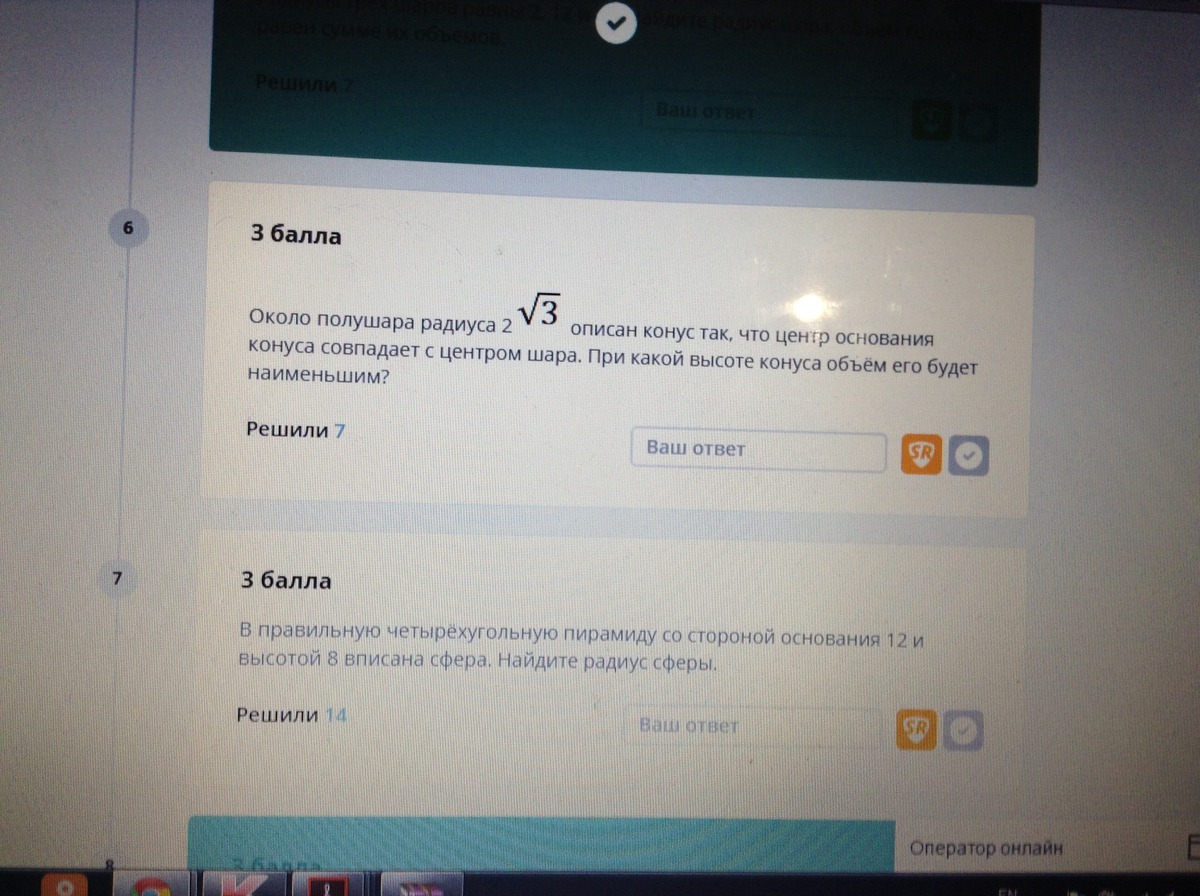
6) V =1/3*πR²*H ;
S =pr ;
1/2* RH =1/2*(R +√(R² +H²))r , где r _радиус полушара.
RH/r - R = √(R² +H²) ;
R²(H/r - 1)² = R² +H² ⇒R² =r²H/(H -2r) .
V =(πr²/3) * H²/(H -2r) ; *** (πr²/3 =k)***
V ' =(πr²/3)*(2H(H-2r) -H²)/(H -2r)² ;
V ' =(πr²/3)*H(H-4r)/(H -2r)² ;
V' + - +
-----------------0 ----------- 2r --------------
V ↑ ↓ min ↑
ответ: H=2r (высота конуса равна диаметру полушара) 4√3 .
*****************************************************
7) апофема пирамиды h =√((a/2)² +H²) =√( (12/2)² +8²) =√(36+64) =10.
Радиус шара равен радиусу вписанной в треугольник окружности 2 стороны
которого = дл апофемы , а третья сторона = дл основ .
S = pr где p полупериметр
12*8/2 =(12+10+10)/2 * r
r =3 .
ответ: 3 .
S =pr ;
1/2* RH =1/2*(R +√(R² +H²))r , где r _радиус полушара.
RH/r - R = √(R² +H²) ;
R²(H/r - 1)² = R² +H² ⇒R² =r²H/(H -2r) .
V =(πr²/3) * H²/(H -2r) ; *** (πr²/3 =k)***
V ' =(πr²/3)*(2H(H-2r) -H²)/(H -2r)² ;
V ' =(πr²/3)*H(H-4r)/(H -2r)² ;
V' + - +
-----------------0 ----------- 2r --------------
V ↑ ↓ min ↑
ответ: H=2r (высота конуса равна диаметру полушара) 4√3 .
*****************************************************
7) апофема пирамиды h =√((a/2)² +H²) =√( (12/2)² +8²) =√(36+64) =10.
Радиус шара равен радиусу вписанной в треугольник окружности 2 стороны
которого = дл апофемы , а третья сторона = дл основ .
S = pr где p полупериметр
12*8/2 =(12+10+10)/2 * r
r =3 .
ответ: 3 .
cos20093:
погоня за баллами вас подводит :). Тут все комментарии удалили, и хорошо, я тоже давал неверный ответ :). Надо найти максимум sin(A)*(cos(A))^2; и H = R/sin(A); A - угол при вершине конуса между осью и образующей. (cos(A))^3 - 2cos(A)*(sin(A))^2=0; (sin(A))^2 = 1/3; H = 6; вот как-то так.
Похожие вопросы
Предмет: Русский язык,
автор: тусисам
Предмет: Английский язык,
автор: Vesna2790
Предмет: Русский язык,
автор: BrainMaps17
Предмет: Русский язык,
автор: vadimdsusupeco
Предмет: Алгебра,
автор: ristekalieva51