Question

площадь прямоугольной трапеции равна 120 см,а ее высота 8 см. найдите все стороны трапеции,если одно из ее оснований на 6 см болльше другого

Answer 1

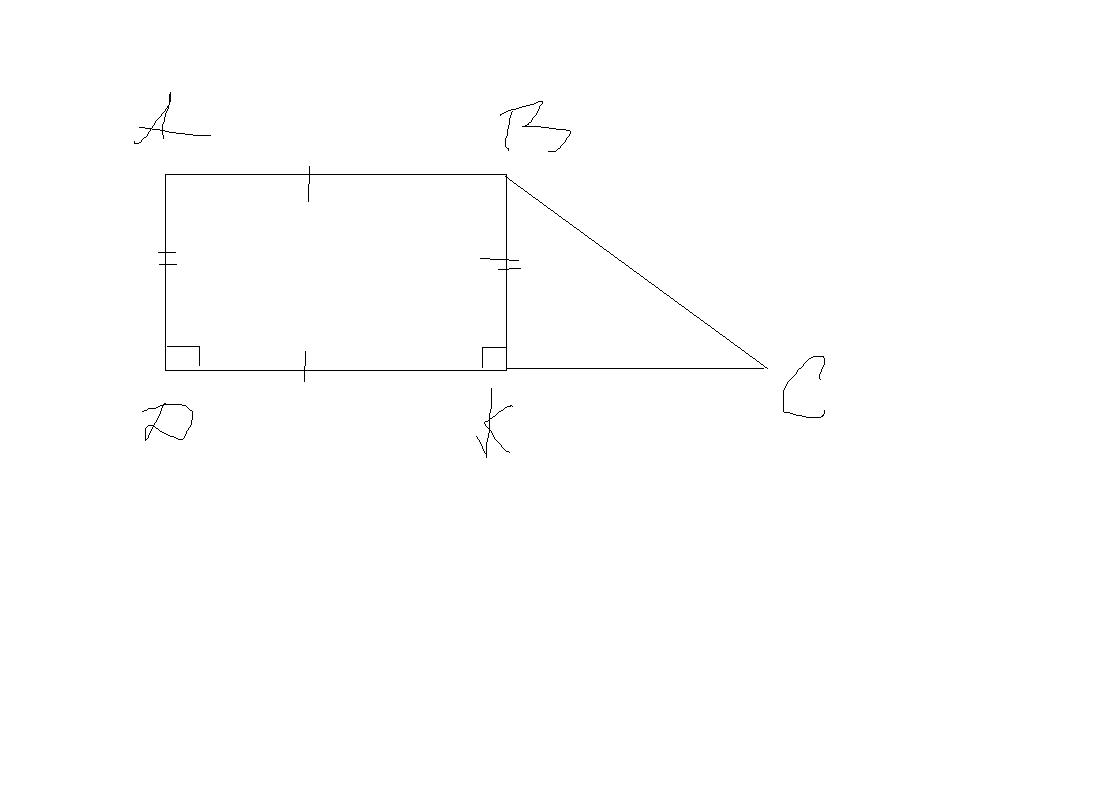
Пусть АВСD - данная прямоугольная трапеция, АВ||CD; AD=8 см, S(ABCD)=120 кв.cм, CD=AB+6

 

Проведем высоту ВК=AD=8 см, тогда ABKD - прямоугольник,  ВКС - прямоугольный треугольник с прямым углом К

AB=DK;

 

Площадь трапеции равна половине произведения суммы ее оснований на высоту:

S(ABCD)=(AB+CD)*AD:2;

(AB+AB+6)*8:2=120;

(2AB+6)*4=120;

2AB+6=120:4;

2AB+6=30;  /:2

AB+3=15;

AB=15-3;

AB=12;

CD=AB+6=12+6=18;

 

DK=CD-DK=18-12=6;

по теореме Пифагора

$BC=sqrt{BK^2+CK^2}=sqrt{8^2+6^2}=\ sqrt{100}=10$

ответ: 12 см,10 см, 18 см, 8 см - стороны трапеции