Предмет: Алгебра,
автор: diana09090
Помогите с производной
Приложения:
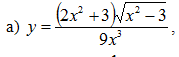
Ответы
Автор ответа:
0
Автор ответа:
0
Похожие вопросы
Предмет: Русский язык,
автор: SonyRay
Предмет: Русский язык,
автор: diadik
Предмет: Русский язык,
автор: лена63кр
Предмет: Химия,
автор: neonflover2005
Предмет: Математика,
автор: ananasik5954