Предмет: Геометрия,
автор: iamjustalina
ДОКАЗАТЬ ТЕОРЕМУ!!!!
Дано:
Многоугольник
окружность вписана в него
ДОКАЗАТЬ: Sмногоугольника=1/2 части * P многоугольника!
Hrisula:
Возможно, S многоугольника равна половине произведения радиуса вписанной окружности на периметр многоугольника?
да,извините,не дописала
Ответы
Автор ответа:
0
Разделяем на треугольники (с общей вершиной в центре окружности).
Высота (проведенные из центра) для всех = r [ (касательные (в данном случае стороны многоугольника) ┴ радиусу в точке касания].
S =S(Δ₁) +S(Δ₂)+₂S(Δ₃) + ... +S(Δn) =a₁*r/2 +a₂*r/2+a₃*r/2 +...+an*r/2 =
=(1/2)*r( a₁ +a₂+a₃ +...+an) = (1/2)*r*P =(P/2)*r.
).
Высота (проведенные из центра) для всех = r [ (касательные (в данном случае стороны многоугольника) ┴ радиусу в точке касания].
S =S(Δ₁) +S(Δ₂)+₂S(Δ₃) + ... +S(Δn) =a₁*r/2 +a₂*r/2+a₃*r/2 +...+an*r/2 =
=(1/2)*r( a₁ +a₂+a₃ +...+an) = (1/2)*r*P =(P/2)*r.
).
Автор ответа:
1
Не скажу, что это доказательство в виде теоремы. Скорее объяснение, которое легко запомнить и передать затем своими словами.
Окружность называется вписанной в многоугольник, если стороны многоугольника являются для неё касательными.
Очевидно, что не во всякий многоугольник можно вписать окружность.
Но всякий многоугольник можно разделить на треугольники.
А площадь треугольника можно найти половиной произведения стороны на высоту, проведенную к ней.
S=0,5*h*a, где а - сторона треугольника, h- высота к ней.
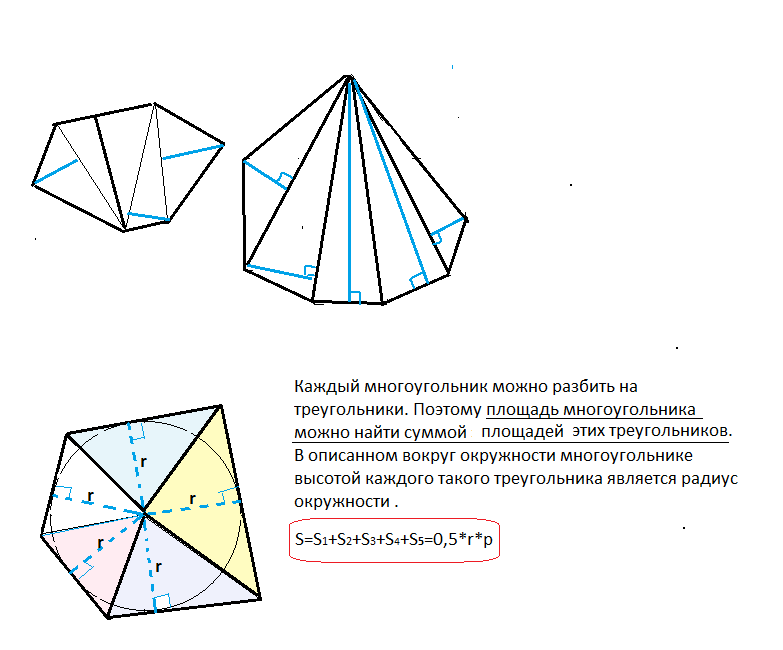
Для многоугольника его площадь - сумма площадей всех треугольников, на которые его можно разделить:
S=S₁+S₂+ S₃ и т.д
Высоты треугольников, на которые можно разделить описанный многоугольник, равны радиусу вписанной окружности, так как радиус перпендикулярен касательной в точке касания. .
Тогда
S=0,5*a₁*r+0,5*a₂*r+0,5*a₃* r+0,5*a₄*r и т.д.
Вынесем общий множитель 0,5r за скобки⇒
S=r*0,5*(a₁+a₂+a₃+a₄+ an)
Ясно, что 0,5*(a₁+a₂+a₃+a₄+an) - это полупериметр многоугольника Теперь можно площадь многоугольника, в который вписана окружность, записать как
S=r*p, где r- радиус вписанной в многоугольник окружности, р- полупериметр этого многоугольника. Что и требовалось доказать.
-----
bzs@
Окружность называется вписанной в многоугольник, если стороны многоугольника являются для неё касательными.
Очевидно, что не во всякий многоугольник можно вписать окружность.
Но всякий многоугольник можно разделить на треугольники.
А площадь треугольника можно найти половиной произведения стороны на высоту, проведенную к ней.
S=0,5*h*a, где а - сторона треугольника, h- высота к ней.
Для многоугольника его площадь - сумма площадей всех треугольников, на которые его можно разделить:
S=S₁+S₂+ S₃ и т.д
Высоты треугольников, на которые можно разделить описанный многоугольник, равны радиусу вписанной окружности, так как радиус перпендикулярен касательной в точке касания. .
Тогда
S=0,5*a₁*r+0,5*a₂*r+0,5*a₃* r+0,5*a₄*r и т.д.
Вынесем общий множитель 0,5r за скобки⇒
S=r*0,5*(a₁+a₂+a₃+a₄+ an)
Ясно, что 0,5*(a₁+a₂+a₃+a₄+an) - это полупериметр многоугольника Теперь можно площадь многоугольника, в который вписана окружность, записать как
S=r*p, где r- радиус вписанной в многоугольник окружности, р- полупериметр этого многоугольника. Что и требовалось доказать.
-----
bzs@
Приложения:
Похожие вопросы
Предмет: Русский язык,
автор: likanerasova
Предмет: Окружающий мир,
автор: monolit324
Предмет: Английский язык,
автор: оващи
Предмет: Геометрия,
автор: ruslanenko37