Question

Решите треугольник по теореме sin и теореме cos 

 

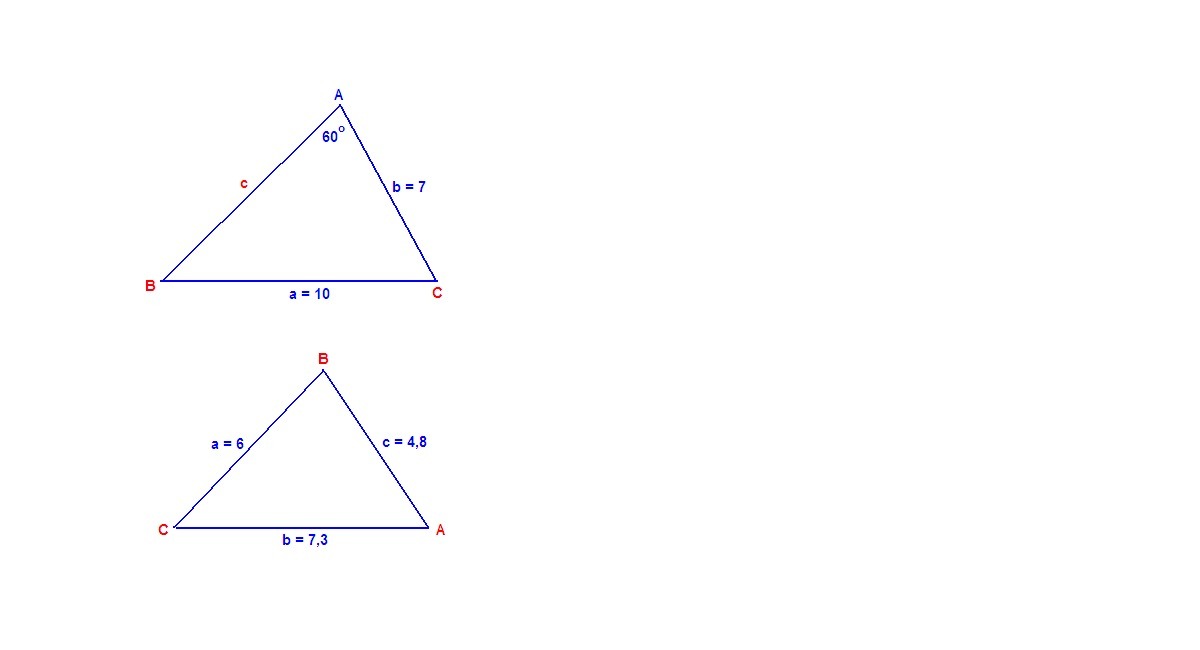
угол А = 60 градусов , a = 10 ; b = 7

 

и по возможности   : 

 

a = 6 , b = 7.3 ; c = 4.8 

 

Нужно полностью решение а не только ответ , заранее спасибо.... 

Answer 1

1. По теореме синусов:
a : sinA = b : sinB
sinB = b · sinA / a
sinB = 7 · sin60° / 10 = 7√3/20 ≈ 0,6062
∠B ≈ 37°

∠C = 180° - ∠A - ∠B ≈ 180° - 60° - 37° ≈ 83°

По теореме синусов:
a : sinA = c : sinC
c = a · sinC / sinA
c ≈ 10 · 0,9925 / 0,866 ≈ 11,5

2.
По теореме косинусов:
b² = a² + c² - 2ac·cosB
cosB = (a² + c² - b²) / (2ac)
cosB = (36 + 23,04 - 53,29) / 57,6
cosB ≈ 0,0998
∠B ≈ 83°

По теореме косинусов:
a² = b² + c² - 2bc·cosA
cosA = (b² + c² - a²) / (2bc)
cosA = (53,29 + 23,04 - 36) / 70,08
cosA ≈ 0,5755
∠A ≈ 54°

∠C = 180° - ∠B - ∠A ≈ 180° - 83° - 54° ≈ 43°