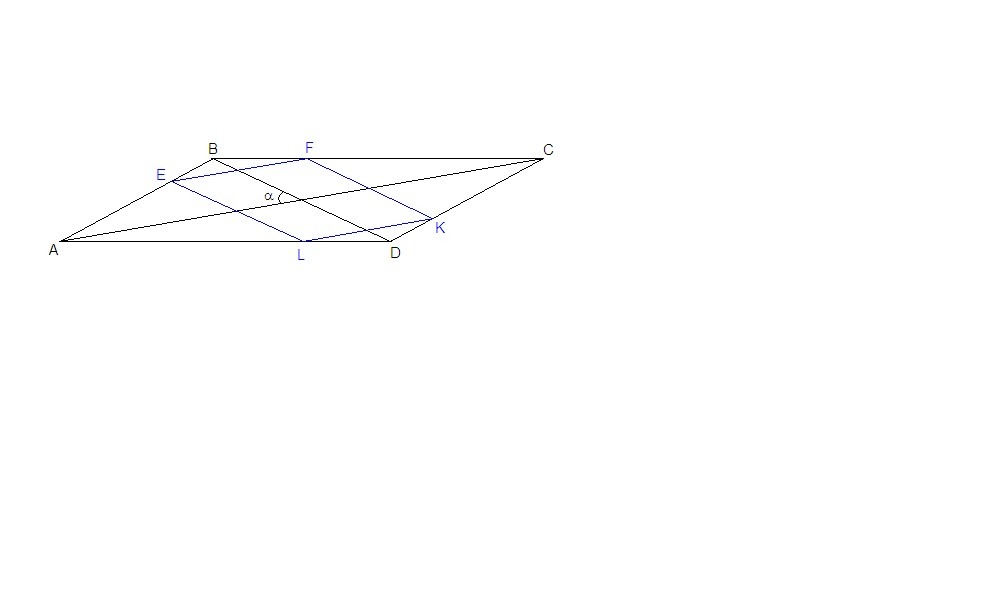
Вершины ромба расположены на сторонах параллелограмма, а стороны ромба параллельны диагоналям параллелограмма. Найдите отношение площадей ромба и. параллелограмма, если отношение диагоналей параллелограмма равно 28.
Ответы
Пусть а - сторона ромба,
d - меньшая диагональ параллелограмма.
BD = d, ⇒ AC = 28d.
Стороны ромба параллельны диагоналям, значит угол между сторонами ромба равен углу между диагоналями (α).
Sромба = а²·sinα
Sabcd = 1/2·AC·BD·sinα = 1/2·28d·d·sinα = 14d²sinα
Sромба : Sabcd = a²/(14d²)
ΔCFK подобен ΔCBD по двум углам (угол при вершине С общий, ∠CFK = ∠CBD как соответственные при пересечении параллельных прямых FK и BD секущей СВ):
CF : CB = FK : BD = a : d (1)
ΔBEF подобен ΔBAC по двум углам (угол при вершине А общий, ∠BEF = ∠BAC как соответственные при пересечении параллельных прямых ЕF и АС секущей АВ):
BF : CB = EF : AC = a : (28d) (2)
Разделим равенство (1) на (2):
CF : BF = 28 : 1, тогда
CF : CB = 28 : 29, значит и
a : d = 28 : 29
Подставим это отношение в отношение площадей:
Sромба : Sabcd = a²/(14d²) = 28² / (14·29²) = 2² · 14² / (14 · 29²) = 4 · 14 / 29²
Sромба : Sabcd = 56/841