Question

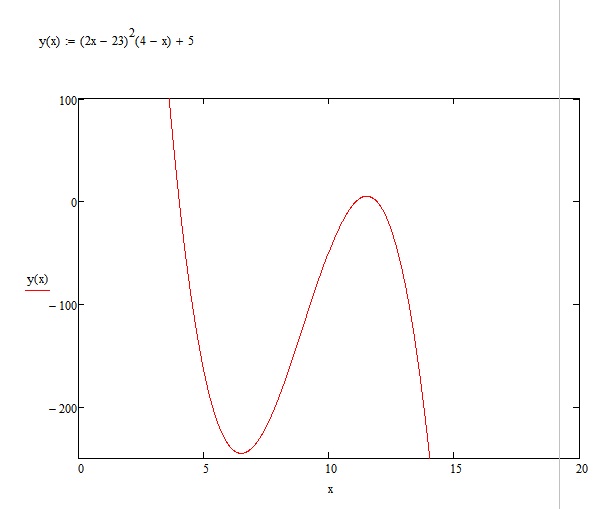
Найти наименьшие значение функции с помощью производной y=(2x-23)^2*(4-x)+5 на промежутке [ 0; 14)

Answer 1

Находим производную:

$y=(2x-23)^{2}(4-x)+5\ y'= ((2x-23)^{2})'(4-x)+(2x-23)^{2}(4-x)'=\=2 cdot (2x-23)(2x-23)'(4-x) -(2x-23)^{2}= \ =4(2x-23)(4-x)-(2x-23)^{2}$

Упростим.

$4(2x-23)(4-x)-(2x-23)^{2}= (2x-23)(4(4-x)-2x+23)=\= (2x-23)(39-6x)$

Найдем периоды возрастания и убывания:

$(2x-23)(39-6x)>0\ 1) left { {{2x-23>0} atop {39-6x>0}} right.\ left { {{x>11,5} atop {x<6,5}} right.\ 2) left { {{2x-23<0} atop {39-6x<0}} right.\ left { {{x<11,5} atop {x>6,5}} right.\ 6,5<x<11,5$</var></p> <p>На промежутке от 6,5 до 11,5 функция возрастает, на остальном она убывает. Имеем две точки экстремума:</p> <p>6,5 - точка минимума</p> <p>11,5 -  точка максимума.</p> <p>У нас пулучается, что функция примет свое наименьшее значение в точке минимума, то есть в точке 6,5. Подставляем в функцию:</p> <p><img src=[/tex]y=(2x-23)^{2}(4-x)+5 = (2cdot 6,5-23)^{2}(4-6,5)+5 = -245" title="(2x-23)(39-6x)>0\ 1) left { {{2x-23>0} atop {39-6x>0}} right.\ left { {{x>11,5} atop {x<6,5}} right.\ 2) left { {{2x-23<0} atop {39-6x<0}} right.\ left { {{x<11,5} atop {x>6,5}} right.\ 6,5<x<11,5" title="y=(2x-23)^{2}(4-x)+5 = (2cdot 6,5-23)^{2}(4-6,5)+5 = -245" title="(2x-23)(39-6x)>0\ 1) left { {{2x-23>0} atop {39-6x>0}} right.\ left { {{x>11,5} atop {x<6,5}} right.\ 2) left { {{2x-23<0} atop {39-6x<0}} right.\ left { {{x<11,5} atop {x>6,5}} right.\ 6,5<x<11,5" alt="y=(2x-23)^{2}(4-x)+5 = (2cdot 6,5-23)^{2}(4-6,5)+5 = -245" title="(2x-23)(39-6x)>0\ 1) left { {{2x-23>0} atop {39-6x>0}} right.\ left { {{x>11,5} atop {x<6,5}} right.\ 2) left { {{2x-23<0} atop {39-6x<0}} right.\ left { {{x<11,5} atop {x>6,5}} right.\ 6,5<x<11,5" />

На промежутке от 6,5 до 11,5 функция возрастает, на остальном она убывает. Имеем две точки экстремума:

6,5 - точка минимума

11,5 -  точка максимума.

У нас пулучается, что функция примет свое наименьшее значение в точке минимума, то есть в точке 6,5. Подставляем в функцию:

$(2x-23)(39-6x)>0\ 1) left { {{2x-23>0} atop {39-6x>0}} right.\ left { {{x>11,5} atop {x<6,5}} right.\ 2) left { {{2x-23<0} atop {39-6x<0}} right.\ left { {{x<11,5} atop {x>6,5}} right.\ 6,5<x<11,5$

На промежутке от 6,5 до 11,5 функция возрастает, на остальном она убывает. Имеем две точки экстремума:

6,5 - точка минимума

11,5 -  точка максимума.

У нас пулучается, что функция примет свое наименьшее значение в точке минимума, то есть в точке 6,5. Подставляем в функцию:

[tex]y=(2x-23)^{2}(4-x)+5 = (2cdot 6,5-23)^{2}(4-6,5)+5 = -245" />

 

График для наглядности.

 

З.Ы. Здесь небольшой подвох есть. В точке х =14, у тоже будет равен -245. Поскольку, в рассматриваемом промежутке [0; 14), точка 14 не включена, то тогда мы не берем ее в расмотрение.