Question

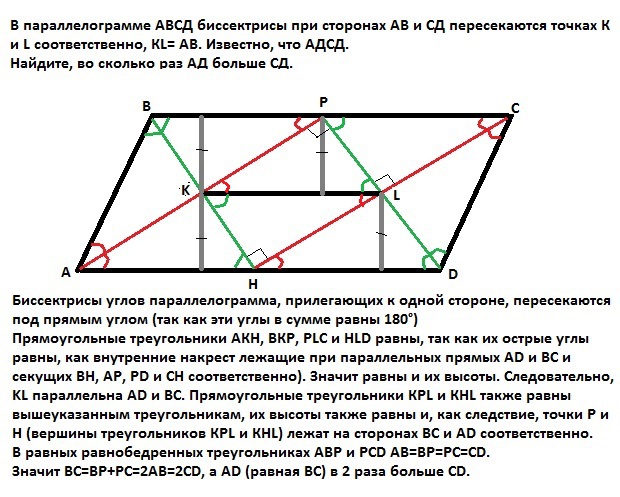
В параллелограмме АВСД биссектрисы при сторонах АВ и СД пересекаются точках К и L соответственно, КL= АВ. Известно, что АД > СД. Найдите, во сколько раз АД больше СД.

Answer 1

Биссектрисы углов параллелограмма, прилегающих к одной стороне, пересекаются под прямым углом (так как эти углы в сумме равны 180°).
Прямоугольные треугольники АКН, ВКР, PLC и HLD равны, так как их острые углы равны, как внутренние накрест лежащие при параллельных прямых AD и ВС и секущих ВН, АР, PD и CH соответственно). Значит равны и их высоты. Следовательно, KL параллельна AD и BC. Прямоугольные треугольники КРL и КНL также равны вышеуказанным треугольникам (так как KL параллельна AD и ВС), их высоты также равны и, как следствие, точки Р и Н (вершины треугольников КРL и КНL) лежат на сторонах ВС и АD соответственно.
В равных равнобедренных треугольниках АВР и PCD АВ=ВР=РС=СD.
Значит ВС=ВР+РС=2АВ=2СD, а AD (равная ВС) в 2 раза больше CD.