1. Решить уравнение: 10^lg2+lg3.
2. Вычислить 10^1+lg5;
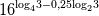
Ответы
1. Если имелось ввиду 10^(lg2 + lg3):
По свойству суммы логарифмов с одинаковымы основаниями: lg2 + lg3 = lg(2*3) = lg6.
10^(lg2 + lg3) = 10^lg6
По основному логарифмическому тождеству: 10^lg6 = 6.
Ответ: 6.
2. 10^(1+lg5)
Представляем 1 как lg10 (lg10 = 1).
10^(1+lg5) = 10^(lg10+lg5)
По свойству суммы логарифмов с одинаковымы основаниями: lg10 + lg5 = lg50.
10^(1+lg5) = 10^(lg10+lg5) = 10^lg50
По основному логарифмическому тождеству: 10^lg50 = 50.
Ответ: 50.
3. 16^(log4(3) - 0.25*log2(3))
По свойству множителя логарифма: 0.25*log2(3) = log(2^4)(3) = log16(3).
По тому же свойству: log4(3) - log16(3) = log4(3) - 0.5*log4(3) = 0.5*log4(3) = log16(3).
По основному логарифмическому тождеству: 16^log16(3) = 3.
Ответ: 3.