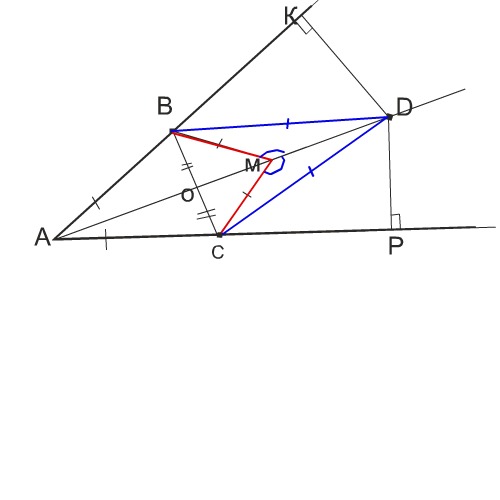
Пожалуйста помогите решить!!! на сторонах угла А отмечены точки В и С так, что АВ=АС.Точка М лежит внутри угла А , и МВ= МС. На прямой АМ отмечена точка D так, что точка М лежит между точками А и D. Докажите, что угол BMD=углу CD.
Ответы
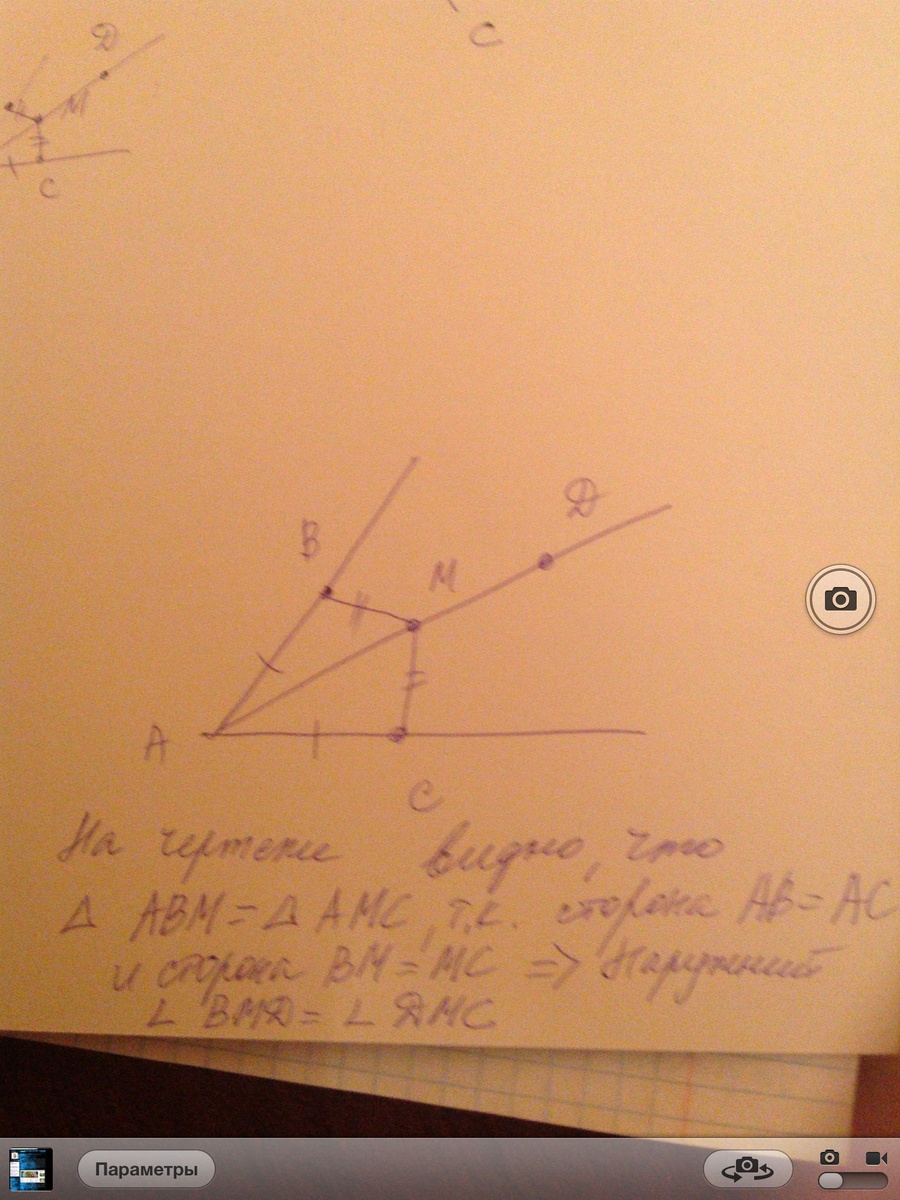
На чертеже видно, что треугольник ВАМ равен треугольнику АМС, так как сторона АВ равна АС и сторона ВМ равна МС. Следовательно наружние углы, примыкающие к треугольникам равны. Соответственно угол ВМD равен углу DC(M)
)Соединим точки В и С.
Так как по условию задачи АВ=ВС и ВМ=МС, треугольники АВС и ВМС - равнобедренные.
АМ делит ВС на два равных отрезка.
ВО=ОС. ⇒АМ - биссектриса угла А
Точка D лежит на биссектрисе АМ, следовательно, на равном расстоянии от сторон угла А. КD=DР
Так как ВО=ОС, ᐃ ВDС - равнобедренный. Сторона ВD=СD, ВМ=СМ по условию задачи, МD - общая .
ᐃ ВDМ= ᐃ ВDС
∠ВМD=∠СМD, что и требовалось доказать.