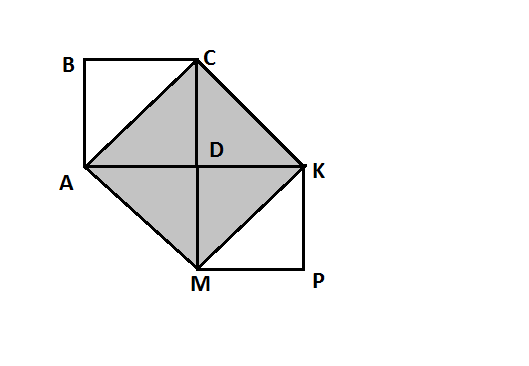
ABCD и MDKP - равные квадраты (рис.) AB=8 см.Найдите площадь и периметр четырёхугольника ACKM.
(Полное решение задачи)
Ответы
Рассмотрим фигуру:
1. АВСD=MDKP- равные квадрату по условию, значит и элементы у них равны( в данном случае стороны): АВ=PK=8 см.
2. У квадрата по свойству все стороны равны, значит АВ=ВС=СD=DA=DM=MK=KP=PD=8 cм
3. Рассмотрим ромб АСКМ, та фигура с которой мы продолжим работать. У этой фигуры, скорее ромба, площадь выражается формулой:
см
4. Идем дальше, периметр- сумма длин всех сторон, а значит P= AC+CK+KM+MA
Так как у этой фигуры равны пары элементов, то AC=CK=KM=MA.
Периметр, точнее вышенаписанные стороны, можно узнать через теорему Пифагора: , тогда
5. P=11.3*4= approx45.2 cм .
Ответ: S=128 см
P= 45.2 cм .