Предмет: Геометрия,
автор: gaziza
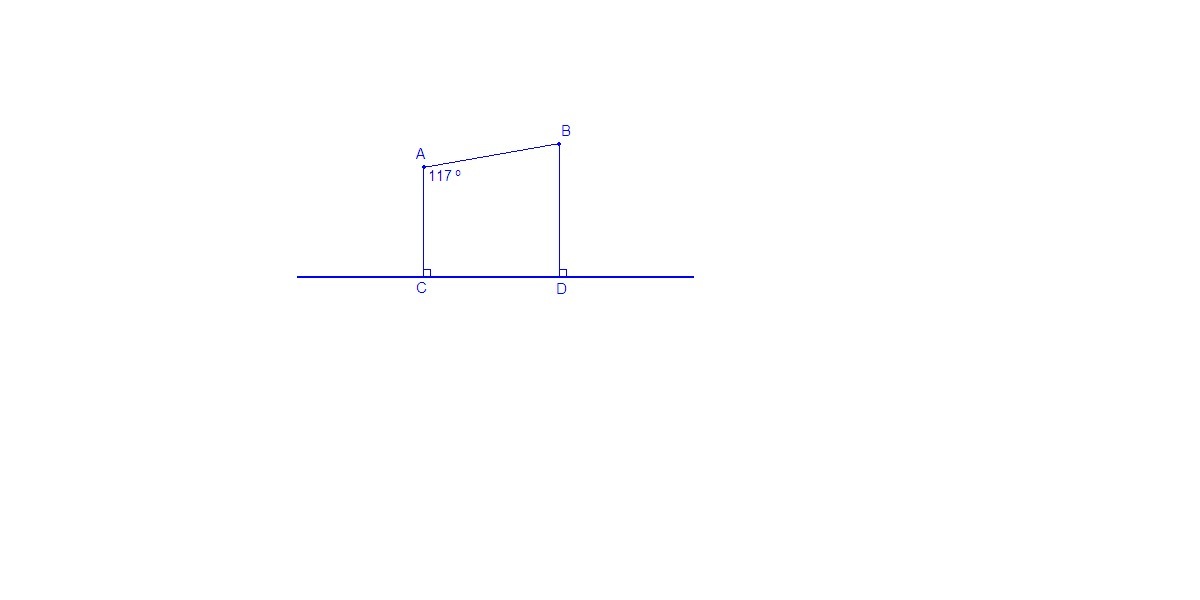
из точек А и В лежащих по одну сторону от прямой,проведены перпендикулярыт АС и ВD к этой прямой: угол ВАС=117 градусов а) найдите угол ABD б) докажите,что прямые АВ и ВD пересекаются.
Ответы
Автор ответа:
0
Два перпендикуляра к одной прямой параллельны:
АС║BD
а)
∠BAC + ∠ABD = 180° так как эти углы внутренние односторонние при пересечении параллельных прямых АС и BD секущей АВ.
∠ABD = 180° - 117° = 63°
б)
Прямые АВ и BD пересекаются, так как имеют общую точку В.
Вероятно, в задаче надо доказать, что прямые АС и BD пересекаются.
∠ВАС и ∠ACD - внутренние односторонние при пересечении прямых АВ и CD секущей АС. Прямые АВ и CD параллельны, если сумма этих углов равна 180°:
∠ВАС + ∠ACD = 117° + 90° = 207°, значит
прямые АВ и CD пересекаются.
АС║BD
а)
∠BAC + ∠ABD = 180° так как эти углы внутренние односторонние при пересечении параллельных прямых АС и BD секущей АВ.
∠ABD = 180° - 117° = 63°
б)
Прямые АВ и BD пересекаются, так как имеют общую точку В.
Вероятно, в задаче надо доказать, что прямые АС и BD пересекаются.
∠ВАС и ∠ACD - внутренние односторонние при пересечении прямых АВ и CD секущей АС. Прямые АВ и CD параллельны, если сумма этих углов равна 180°:
∠ВАС + ∠ACD = 117° + 90° = 207°, значит
прямые АВ и CD пересекаются.
Приложения:
Похожие вопросы
Предмет: Русский язык,
автор: Аноним
Предмет: Математика,
автор: madinartai45
Предмет: Алгебра,
автор: latifashindy
Предмет: Математика,
автор: nata1977
Предмет: Алгебра,
автор: Yulka2011