Предмет: Геометрия,
автор: karakatica2001
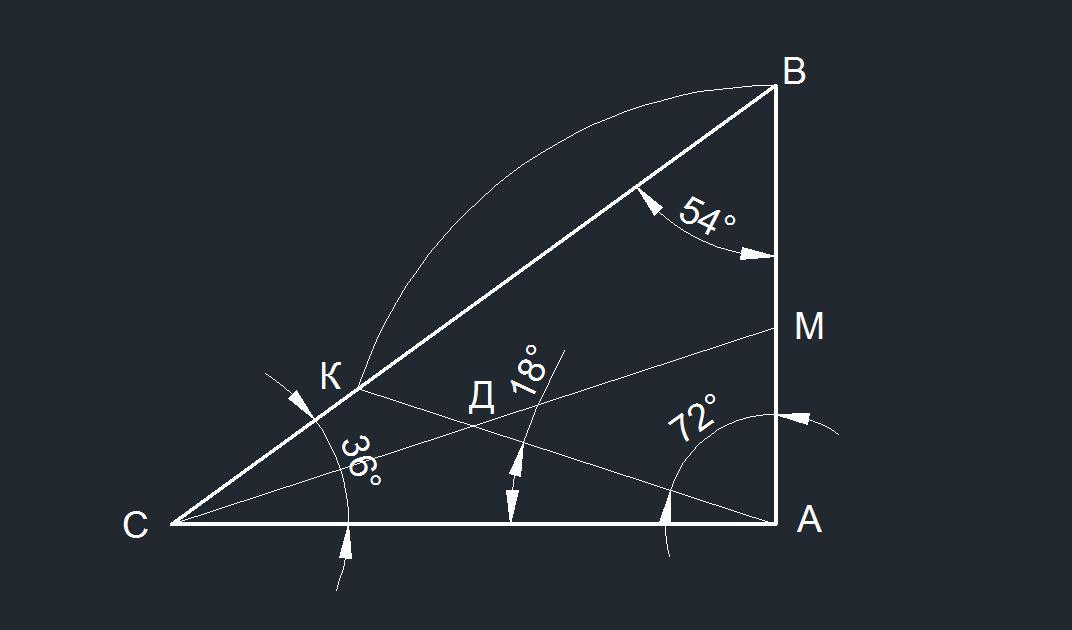
На гипотенузе AB прямоугольного треугольника ABC выбрана точка К ,для которой CK=BC.Отрезок CK пересекает биссектрису AM в её середине.Найти углы треугольника ABC
Ответы
Автор ответа:
4
Обозначим середину биссектрисы угла А точкой Д, а половину угла А - α.
Для прямоугольного треугольника АМС сторона АМ - гипотенуза. Её середина равноудалена от вершин, тогда АД = ДС и угол ДСА равен α, а угол ДСМ = 90 - α.
Угол В = 90 - 2α, но так как СВ = СК, то и угол ВКС = 90 - 2α.
Рассмотрим треугольник КСВ. В нём угол КСВ = 180-2*(90-2α) = 4α.
Получаем для угла ДСМ 90 - α = 4α.
Отсюда 5α = 90 α = 90 / 5 = 18°.
Тогда острые углы треугольника АВС равны:
Угол А = 2*18 = 36°,
угол В = 90 - 36 = 54°.
Для прямоугольного треугольника АМС сторона АМ - гипотенуза. Её середина равноудалена от вершин, тогда АД = ДС и угол ДСА равен α, а угол ДСМ = 90 - α.
Угол В = 90 - 2α, но так как СВ = СК, то и угол ВКС = 90 - 2α.
Рассмотрим треугольник КСВ. В нём угол КСВ = 180-2*(90-2α) = 4α.
Получаем для угла ДСМ 90 - α = 4α.
Отсюда 5α = 90 α = 90 / 5 = 18°.
Тогда острые углы треугольника АВС равны:
Угол А = 2*18 = 36°,
угол В = 90 - 36 = 54°.
Приложения:
Похожие вопросы
Предмет: Русский язык,
автор: sasha9452
Предмет: Английский язык,
автор: Аноним
Предмет: Английский язык,
автор: Twinsister11
Предмет: История,
автор: Sashka2211
Предмет: Математика,
автор: kerosinskayak