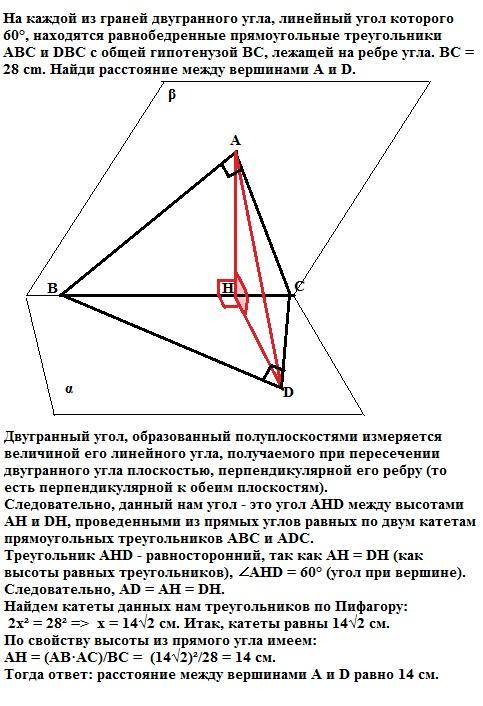
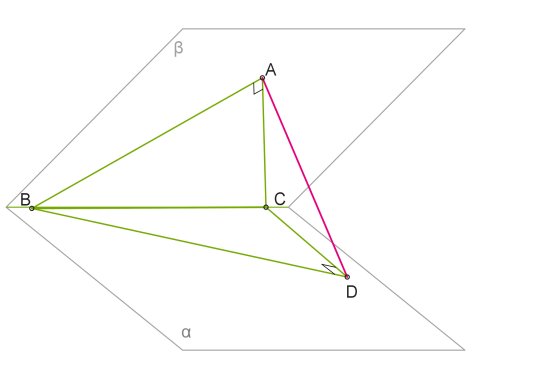
На каждой из граней двугранного угла, линейный угол которого60 градусов, находятся равнобедренные прямоугольные треугольники ABC и DBC с общей гипотенузой BC, лежащей на ребре угла. BC = 28 cm. Найди расстояние между вершинами A и D
Ответы
Ответ:
AD = 14 см.
Объяснение:
Двугранный угол, образованный полуплоскостями измеряется величиной его линейного угла, получаемого при пересечении двугранного угла плоскостью, перпендикулярной его ребру (то есть перпендикулярной к обеим плоскостям).
Следовательно, данный нам угол - это угол АНD между высотами АН и DH, проведенными из прямых углов равных по двум катетам прямоугольных треугольников АВС и ADC.
Треугольник AHD - равносторонний, так как АН = DH (как высоты равных треугольников), ∠AHD = 60° (угол при вершине).
Следовательно, AD = AH = DH.
Найдем катеты данных нам треугольников по Пифагору:
2х² = 28² => х = 14√2 cм. Итак, катеты равны 14√2 cм.
По свойству высоты из прямого угла имеем:
АН = (АВ·АС)/ВС = (14√2)²/28 = 14 см.
Тогда ответ: расстояние между вершинами A и D равно 14 см.