Question

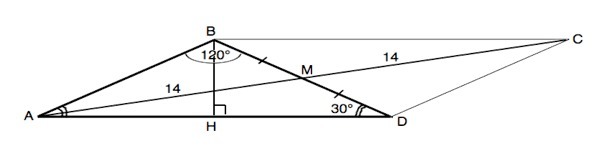
Найдите боковые стороны равнобедренного треугольник, если угол между ними равен 120 градусов, а медиана, проведенная к боковой стороне, равна 14см

Answer 1

Обозначим данный треугольник АВD. 

Примем его боковые стороны равными а. 

Проведем высоту ВН. 

В равнобедренном треугольнике с углом при вершине 120° углы при основании равны 30°. ⇒

АН=DH=а•cos30°=a√3/2⇒   AD=a√3

Продлим медиану АМ на её длину до т.С. 

АС=2 АМ=28. 

Соединим В и D с т.С. 

ВМ=DM по условию, АМ=МС по построению. Диагонали четырехугольника АВСD точкой пересечения делятся пополам. ⇒ АВСD – параллелограмм (по признаку).

По свойству параллелограмма сумма квадратов диагоналей равна сумме квадратов ВСЕХ его сторон. 

Противоположные стороны параллелограмма равны. 

АС²+BD²= 2 АВ²+2ВС² 

28²+а²=2а²+6а²⇒

 7а²=28•28

а²=4•4•7

а=4√7 см – длина боковых сторон треугольника.