Question

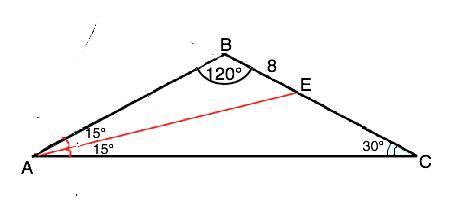
В треугольнике ABC AB=BC, угол CAB=30°, AE - биссектриса, BE=8 см. Найдите площадь треугольника ABC. ответ должен получиться примерно равным 75,7 см^2

Answer 1

 АЕ - биссектриса. ⇒ ∠ВАЕ=∠ЕАС=30°:2=15°. ⇒ ∠ВЕА=180°-120°-15°=45°

По т.синусов АВ/sin45°=BE/sin15°.

sin 45°=1/√2; sin 15°=(√3-1)/2√2 (по таблице)⇒ АВ√2=8•2√2/(√3-1)  AB=16/(√3-1). Домножив числитель и знаменатель дроби на (√3+1), получим АВ=16(√3+1)/(√3-1)•(√3+1)=8(√3+1).

S(ABC)=AB•BC•sinABC/2 => S(ABC)=[8(√3+1)]²•√3/4=32√3( 2+√3) см²