Question

Помогите с геометрией, срочно, прошу!
1. В правильной пирамиде SABC с высотой SH и ребром основания AB=a угол между боковым ребром и плоскостью основания равен α . Найдите площадь сечения пирамиды плоскостью, проходящей через точку H параллельно ребрам SA и BC!

Answer 1

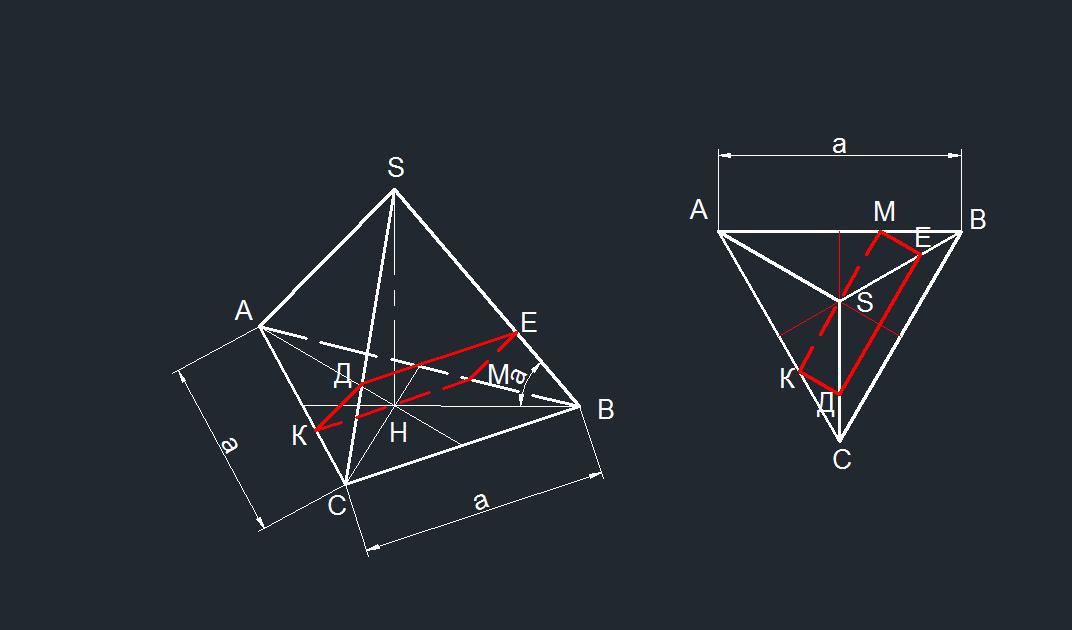
Отрезок высоты основания ВН = 2/3 высоты треугольника основания.
h = а√3/2 (свойство медиан треугольника). ВН =а/√3.
Тогда наклонное ребро пирамиды равно BS = BH / cos α = a / √3cos α.
Плоскость, проходящая через точку H параллельно ребрам SA и BC, образует прямоугольник так как стороны КМ и ДЕ равны 2/3 стороны основания и углы прямые. КМ = 2а / 3.
Сторона КД = (1/3) BS =  a / 3√3cos α.
Отсюда S = 2а² / (9√3cos α).