Предмет: Алгебра,
автор: AnnaZueva1234
Три вершины правильного 10-угольника покрасили в рыжий цвет, а остальные-в черный. Сколько можно провести отрезков с рыжими концами?
Пожалуйста с подробным решением.
Ответы
Автор ответа:
2
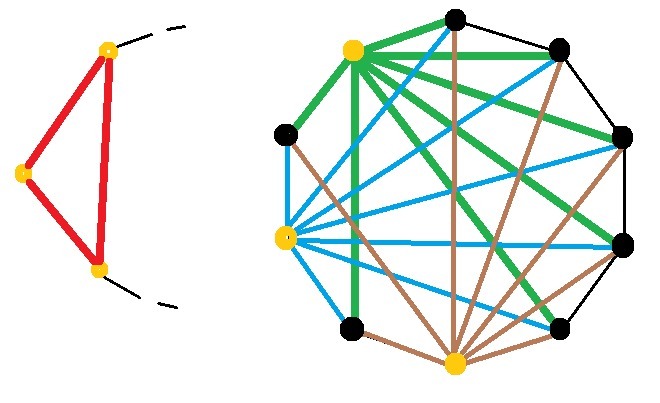
1. Оба конца отрезка рыжего цвета.
Только 3 отрезка можно провести через 3 рыжие вершины, чтобы оба конца были рыжими.
2. Только один конец отрезка рыжего цвета.
Из каждой рыжей вершины можно провести 7 отрезков к черным вершинам. Из трёх рыжих вершин можно провести
3 * 7 = 21 отрезок с разноцветными концами
3. Хотя бы один конец отрезка рыжего цвета.
21 + 3 = 24 отрезка всего можно провести, соединив рыжие вершины либо с рыжими, либо с чёрными
Только 3 отрезка можно провести через 3 рыжие вершины, чтобы оба конца были рыжими.
2. Только один конец отрезка рыжего цвета.
Из каждой рыжей вершины можно провести 7 отрезков к черным вершинам. Из трёх рыжих вершин можно провести
3 * 7 = 21 отрезок с разноцветными концами
3. Хотя бы один конец отрезка рыжего цвета.
21 + 3 = 24 отрезка всего можно провести, соединив рыжие вершины либо с рыжими, либо с чёрными
Приложения:
Похожие вопросы
Предмет: Русский язык,
автор: Arsik8379
Предмет: Русский язык,
автор: Death8800
Предмет: Русский язык,
автор: olgapetrovaaaaa
Предмет: Музыка,
автор: miuabatir
Предмет: Алгебра,
автор: sasha154634