Question

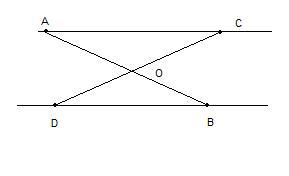
Равные отрезки АВ и CD пересекаются в точке О,причём АС||BD.Докажите,что треугольник BOD равнобедренный.

Answer 1

АС||BD по условию. Используем теорему: если две параллельные прямые (в нашем случае это АС и BD) пересечены секущей (СD), то накрест лежащие углы (это ACD и BDC) равны. При пересечении этих же параллельных прямых секущей АВ накрест лежащие углы САВ и DBA также равны. Значит, треугольники АОС и BOD подобны по первому признаку подобия: два угла одного треуг-ка соответственно равны двум углам другого.
Для подобных треуг-ов запишем соотношение сходственных сторон:
АО : BO = CO : DO. 
AO = AB - BO, CO = CD - DO. Т.к. АВ=CD, можно записать, что 
CO=AB -  DO.
Подставим это  в выражение отношения сходственных сторон:
(AB - BO) : BO = (AB - DO) : DO
DO*(AB - BO) = BO*(AB - DO)
DO*AB - DO*BO = BO*AB - BO*DO
DO*AB=BO*AB
DO=BO, треугольник BOD - равнобедренный