Question

На биссектрисе CL треугольника ABC выбрана точка K. Оказалось, что AC+AK=CB. Докажите что угол CAK=2*уголCBK.

Answer 1

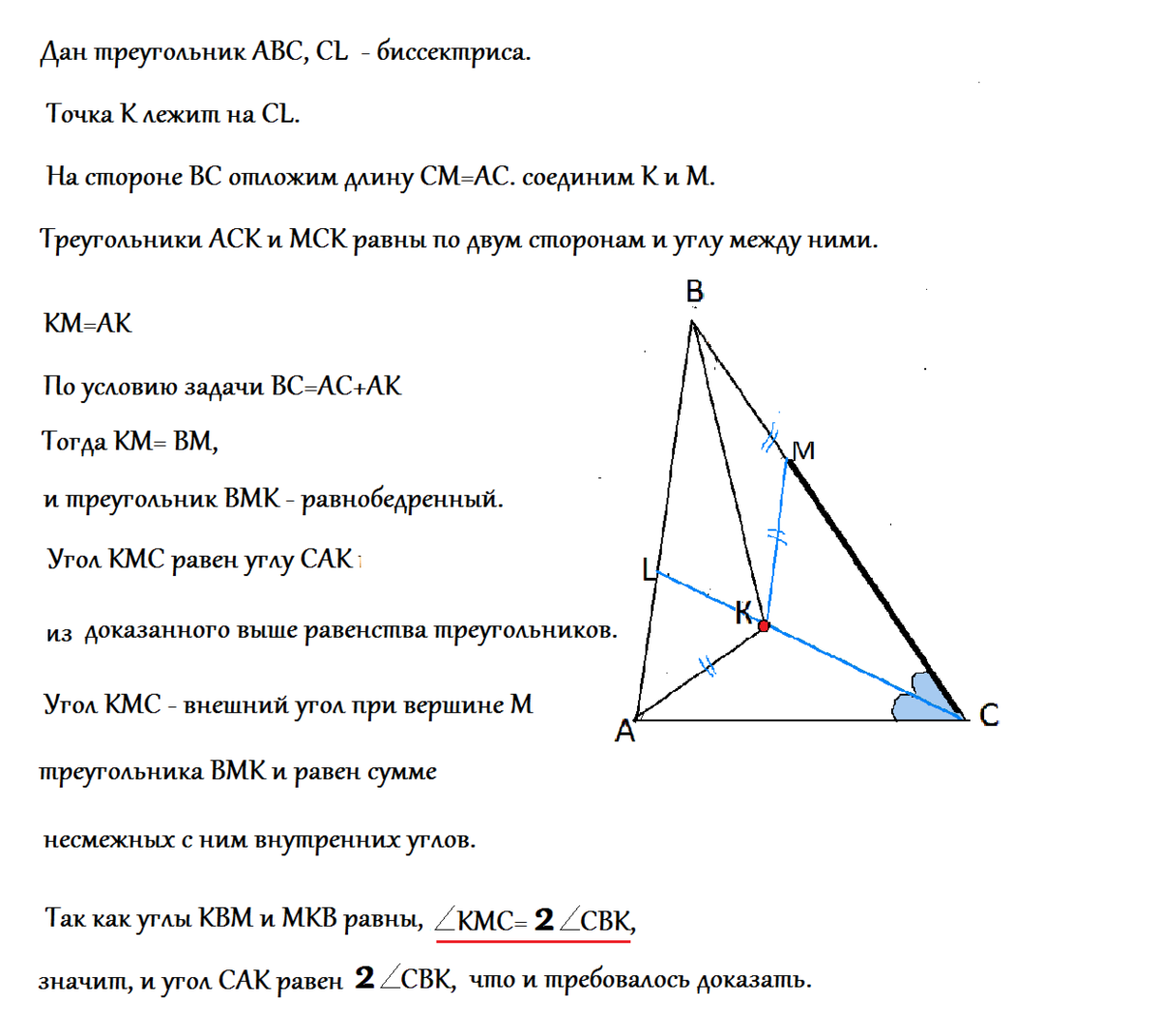
Дан треугольник АВС, СL  - биссектриса.
Точка К лежит на CL.
Сделаем рисунок.  
На стороне ВС отложим длину СМ=АС.
Соединим К и М. 
Треугольники АСК и МСК равны по двум сторонам и углу между ними. КМ=АК
По условию задачи ВС=АС+АК
Тогда КМ= ВМ,  и треугольник ВМК - равнобедренный. 
Угол КМС равен углу САК из доказанного выше равенства треугольников. 
Угол КМС - внешний угол при вершине М треугольника ВМК и равен сумме несмежных с ним внутренних углов. 
Так как углы КВМ и МКВ равны, ∠ КМС=2∠СВК, а значит, что и
 ∠САК равен 2∠СВК, что и требовалось доказать.