Question

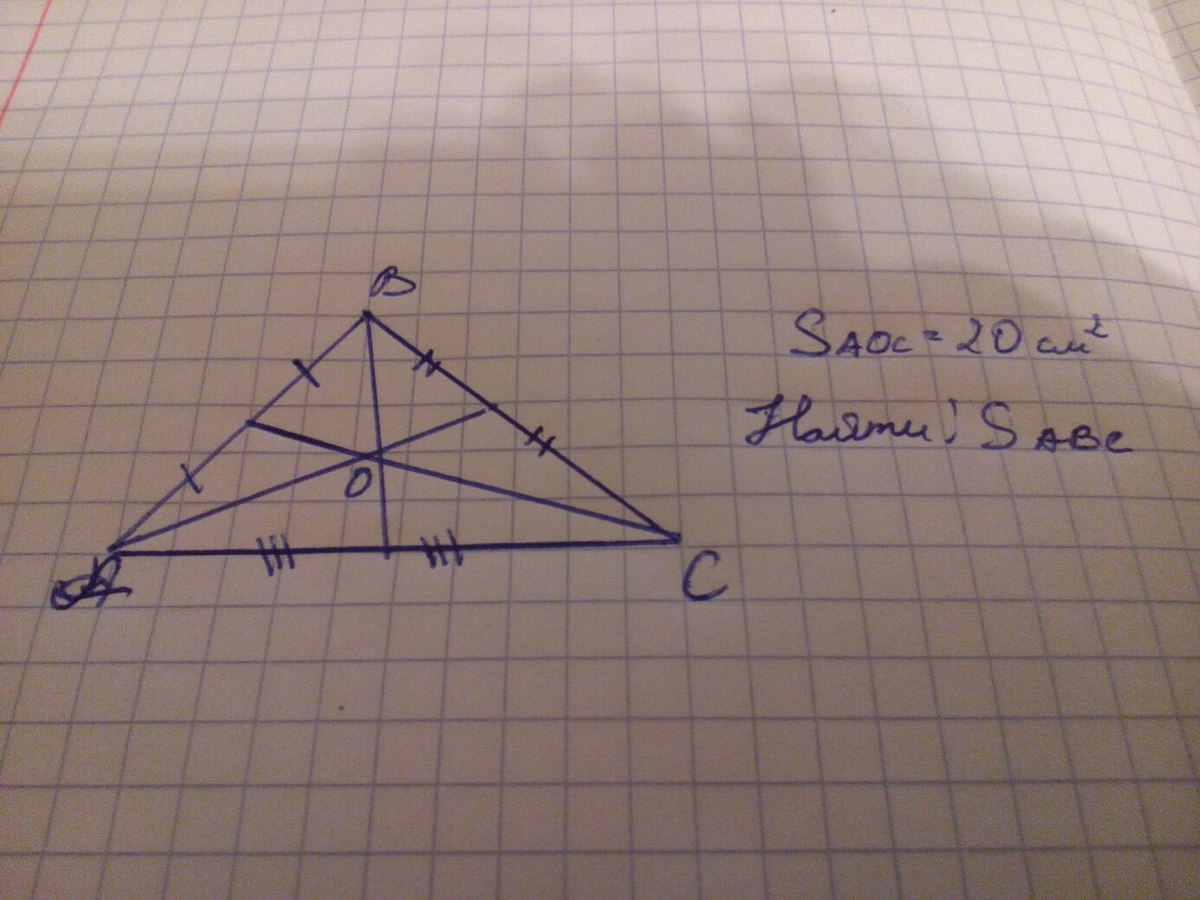
Срочно! В произвольном треугольнике АВС медианы пересекаются в точке О, площадь треугольника АОС = 20, найти площадь треугольника АВС.

Answer 1

Медиана ВМ разделила треугольник АВС на 2 равновеликих треугольника АВМ и СВМ. АО делит треугольник АВМ на треугольники АОМ и АОВ,имеющие общую высоту,причем ВО в 2 раза больше ОМ,т.к . медианы в точке пересечения делятся в отношении 2:1 от вершины.Тогда площадь АОВ равна 2 площадям АОМ.Значит площадь АОМ равна 1/6 площади АВС.Аналогично площадь СОМ равна также 1/6 площади АВС.
S(AOM)+S(COM)=S(FOC)=1/6S(ABC)+1/6S(ABC)=1/3S(ABC)=20⇒
S(ABC)=20*3=60см²