Предмет: Геометрия,
автор: Kuzinatra
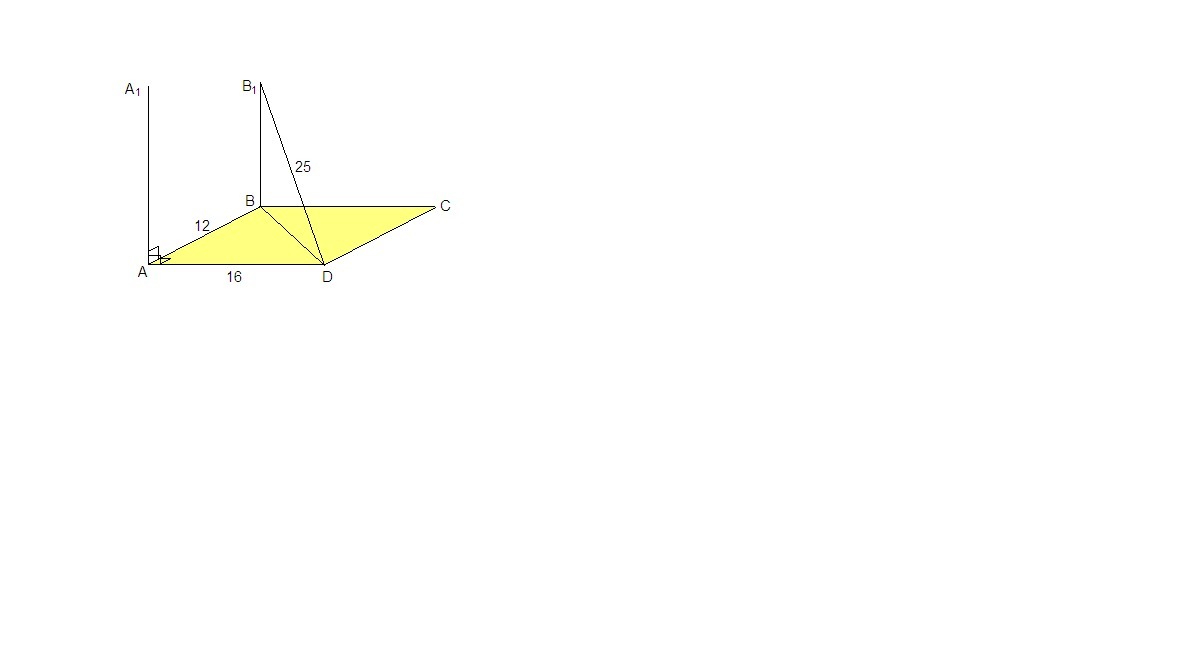
Через вершины А и В прямоугольника АВСД проведены параллельные прямые А1А и В1В, не лежащие в плоскости прямоугольника. Известно, что АА1 перпендикулярно АВ и А1А перпендикулярно АД.Найти В1В, если В1Д=25 см, АВ = 12 см, АД=16 см
Ответы
Автор ответа:
0
ABCD прямоугольник, поэтому в ΔABD ∠BAD = 90°.
По теореме Пифагора
BD = √(AB² + AD²) = √(144 + 256) = √400 = 20 см.
АА₁ ⊥ АВ, АА₁ ⊥ AD, ⇒ АА₁ ⊥ (ABC)
BB₁ ║ AA₁, ⇒ BB₁ ⊥ (ABC)
Тогда в ΔBB₁D ∠B₁BD = 90°.
По теореме Пифагора
BB₁ = √(B₁D² - BD²) = √(625 - 400) = √225 = 15 см
По теореме Пифагора
BD = √(AB² + AD²) = √(144 + 256) = √400 = 20 см.
АА₁ ⊥ АВ, АА₁ ⊥ AD, ⇒ АА₁ ⊥ (ABC)
BB₁ ║ AA₁, ⇒ BB₁ ⊥ (ABC)
Тогда в ΔBB₁D ∠B₁BD = 90°.
По теореме Пифагора
BB₁ = √(B₁D² - BD²) = √(625 - 400) = √225 = 15 см
Приложения:
Похожие вопросы
Предмет: Другие предметы,
автор: andrey15072006
Предмет: Другие предметы,
автор: sakenabdigalim09
Предмет: Қазақ тiлi,
автор: daniyar2601zh
Предмет: Химия,
автор: Nastenka123