Предмет: Геометрия,
автор: girfanovmaksim
Помогите с задачей! Стороны треугольника равны 3,4,5. Найдите площади вписанного в треугольник и описанного около него кругов.
Ответы
Автор ответа:
14
решение прилагается на фото
Приложения:
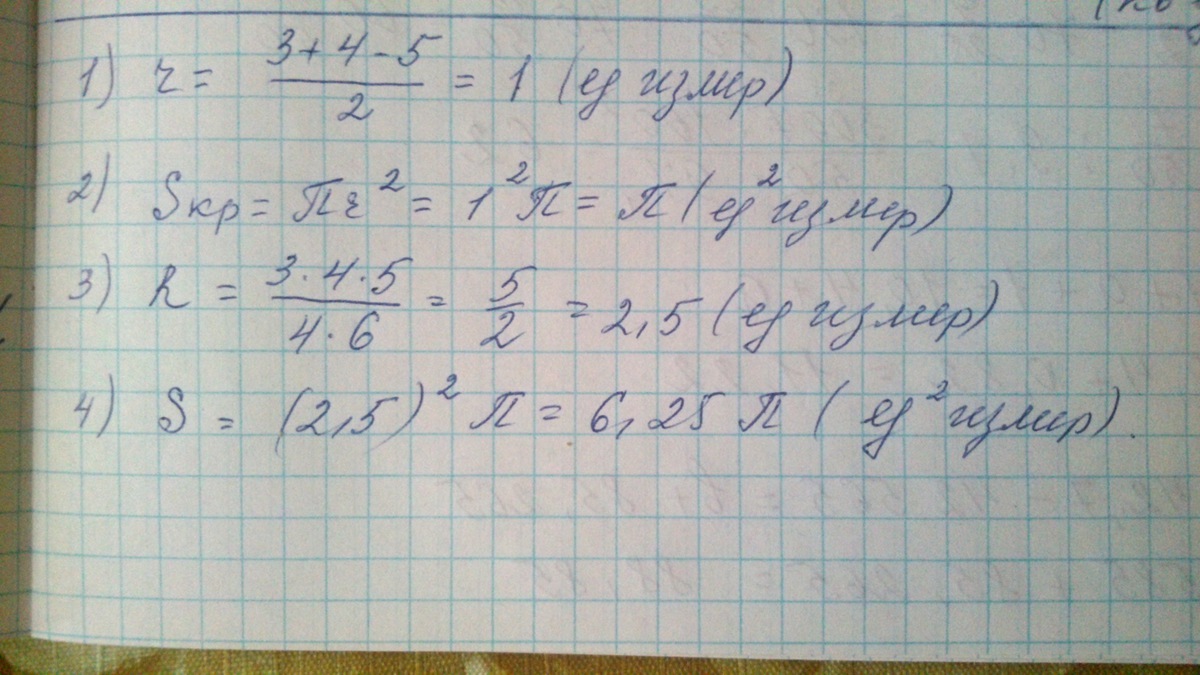
Автор ответа:
13
Данный треугольник - прямоугольный. Это видно из отношения сторон
3:4:5 - отношения сторон так называемого «египетского» прямоугольного треугольника.
Радиус описанной вокруг прямоугольного треугольника окружности равен половине гипотенузы.
R=5:2=2,5
Радиус вписанной в прямоугольный треугольник окружности находят по формуле:
r=(а+b-c):2, где а и b - катеты, с - гипотенуза.
r=( 7-5):2=1
Площадь круга находим по формуле:
S=πr²
S (опис)= π R²=π*6, 25 (единиц площади)
S (впис)=πr²= π*1²=π ( единиц площади)
3:4:5 - отношения сторон так называемого «египетского» прямоугольного треугольника.
Радиус описанной вокруг прямоугольного треугольника окружности равен половине гипотенузы.
R=5:2=2,5
Радиус вписанной в прямоугольный треугольник окружности находят по формуле:
r=(а+b-c):2, где а и b - катеты, с - гипотенуза.
r=( 7-5):2=1
Площадь круга находим по формуле:
S=πr²
S (опис)= π R²=π*6, 25 (единиц площади)
S (впис)=πr²= π*1²=π ( единиц площади)
Похожие вопросы
Предмет: Русский язык,
автор: умк2
Предмет: Английский язык,
автор: tomat551
Предмет: Английский язык,
автор: иван1109
Предмет: Алгебра,
автор: 02101920