Предмет: Алгебра,
автор: КолянФ
ПОМОГИТЕ РЕШИТЬ!!! ХОТЯ БЫ ПРЕОБРАЗОВАТЬ!
Приложения:
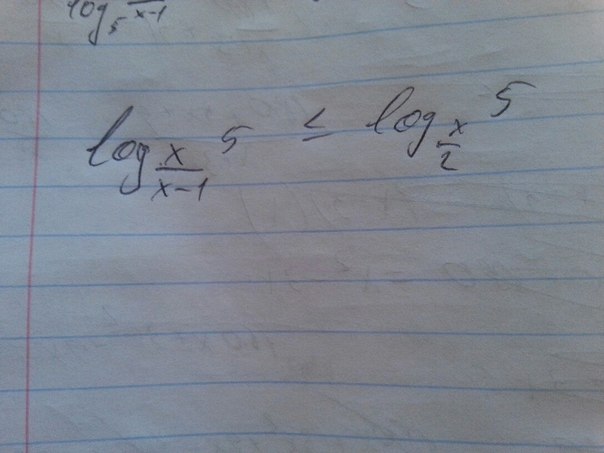
Ответы
Автор ответа:
1
ОДЗ: хЄ(1,2)U(2,+беск)
КолянФ:
а разве так можно взять и убрать единицу в числителе?
Никто просто так 1 в числителе не убирал. Здесь сравниваются дроби с одинаковыми числителями (больше та, у которой знаменатель меньше)...
Например, если сравнить две дроби: 1/2 и 1/5, то 1/2 > 1/5, так как 2<5 .
Похожие вопросы
Предмет: Русский язык,
автор: Фотимагуль
Предмет: Другие предметы,
автор: школьник619
Предмет: Русский язык,
автор: wew12
Предмет: Математика,
автор: ioreyou211