Предмет: Геометрия,
автор: Miiia
Комната имеет форму куба. Паук, сидящий в середине ребра, хочет, двигаясь по кратчайшему пути, поймать муху, сидящую в одной из самых удаленных от паука вершин куба. Как должен двигаться паук?
решите пожалуйста как можно подробнее)
Матов:
перезагрузи страницу если не видно
Ответы
Автор ответа:
2
Пусть наш куб  имеет длину ребра
имеет длину ребра  , середина точка
, середина точка  ,
,  так как самая удаленная вершина всегда будет симметрична , какую бы точку не взять на середине ребра данного куба , рассмотрим когда точка лежит , на ребре
так как самая удаленная вершина всегда будет симметрична , какую бы точку не взять на середине ребра данного куба , рассмотрим когда точка лежит , на ребре 
Теперь надо понять как он должен двигаться , с начало в какую сторону , видно что самое удаленная вершина это точка , так же и другая есть симметричная ей
, так же и другая есть симметричная ей  , но будет рассматривать
, но будет рассматривать  .
.
так как то есть можно не рассматривать вариант когда паук ползет в сторону
то есть можно не рассматривать вариант когда паук ползет в сторону  , рассмотрим вариант когда он ползет к стороне
, рассмотрим вариант когда он ползет к стороне  , когда паук ползет к вершине
, когда паук ползет к вершине  , очевидно что расстояние равно
, очевидно что расстояние равно  , пусть есть некая точка
, пусть есть некая точка  , которая принадлежит
, которая принадлежит  , по неравенству треугольников
, по неравенству треугольников 
выразим расстояние , когда паук ползет через точку
она равна
получили функцию
которая имеет критическую точку (находится через производную ) , минимум
(находится через производную ) , минимум  , что меньше выше сказанного расстояния
, что меньше выше сказанного расстояния
Ответ Паук должен с начало придти к , потом к
, потом к  это есть кратчайшее расстояние
это есть кратчайшее расстояние
Теперь надо понять как он должен двигаться , с начало в какую сторону , видно что самое удаленная вершина это точка
так как
выразим расстояние , когда паук ползет через точку
она равна
получили функцию
которая имеет критическую точку
Ответ Паук должен с начало придти к
Приложения:
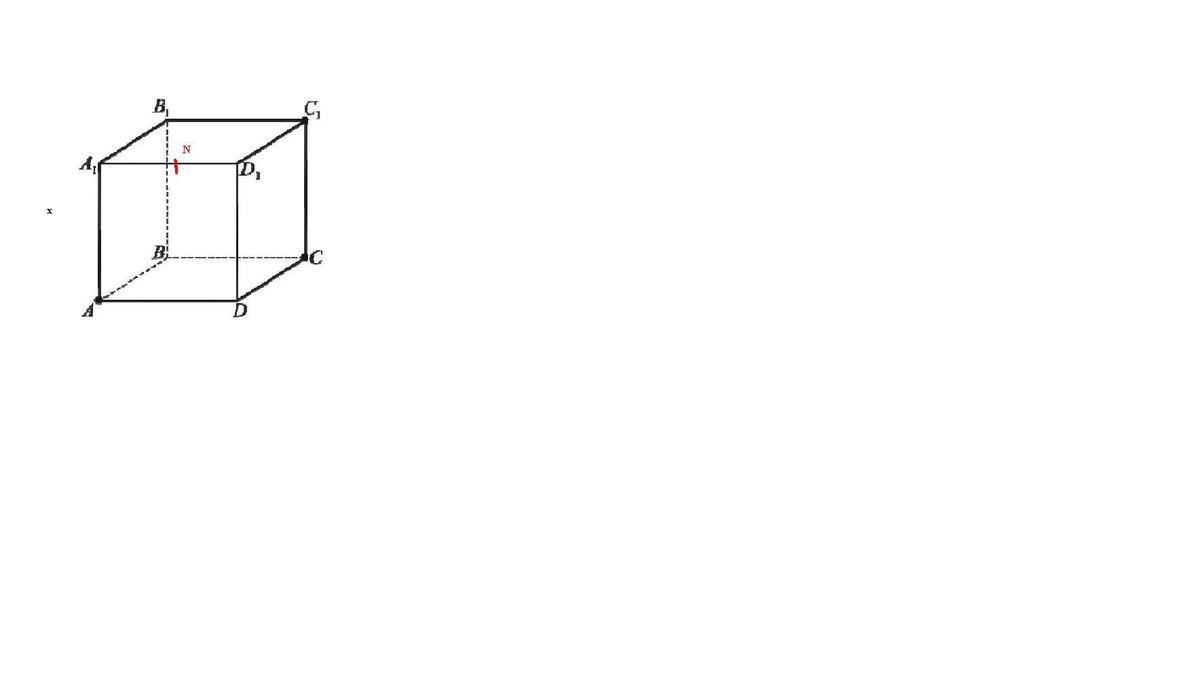
Похожие вопросы
Предмет: Русский язык,
автор: roma25776
Предмет: Русский язык,
автор: Катюшка024
Предмет: Қазақ тiлi,
автор: умка5551
Предмет: Другие предметы,
автор: miiimi
Предмет: Физика,
автор: nastya2019m