Question

Вычислите сторону правильного треугольника, описанного около окружности радиуса 3 см

Answer 1

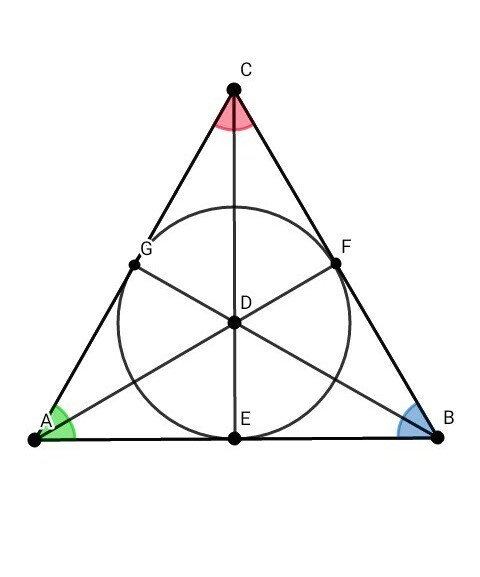
ДАНО: ∆ АВС — равносторонний ; вписанная окружность ( D ; r ) ; DE = 3 см.

НАЙТИ: АВ
_________________________

РЕШЕНИЕ:

1) Центром вписанной окружности любого треугольника является точка пересечения биссектрис. Но по условию ∆ АВС равносторонний =>

!!! "Биссектрисы равностороннего треугольника являются и высотой, и медианой" !!!

Значит, угол ABG = угол CBG = 1/2 × угол АВС = 1/2 × 60° = 30°

2) Рассмотрим ∆ BDE ( угол DEB = 90° ):

Катет, лежащий против угла в 30°, равен половине гипотенузы.

BD = 2 × DE = 2 × 3 = 6 см

По теореме Пифагора:

BD² = DE² + BE²

BE² = 6² - 3² = 36 - 9 = 27

BE = 3√3 см

Значит, АВ = 2 × ВЕ = 2 × 3√3 = 6√3 с
_____________________________

Есть другой метод решения данной задачи:

Воспользуемся формулой для нахождения стороны равностороннего треугольника через известный радиус вписанной окружности.

$a = 2 sqrt{3 } times r \ a = 2 sqrt{3} times 3 = 6 sqrt{3}$

где а - это сторона равностороннего треугольника, r - радиус вписанной окружности

ОТВЕТ: AB = 6√3 см