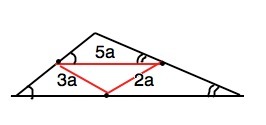
стороны треугольника относятся как 2:3:5 а периметр треугольника образованного его средними линиями равен 40 см.Найдите средние линии треугольника
Ответы
Даётся решение, но обязательно !!! прочитайте примечание после него.
Средние линии треугольника параллельны стороне, которую не пересекают. При этом соответственные углы, которые получаются при пересечении параллельных сторон третьей, равны.
Треугольник, образованный средним линиями исходного треугольника, подобен ему. Поэтому отношение сторон обоих треугольников одинаково.
Периметр треугольника, образованного средними линиями, 40 см,
его стороны относятся как 2:3:5.
Примем коэффициент отношения сторон равным а. тогда периметр меньшего треугольника 2а+3а+5а=10а ⇒
10а=40
а=4 см
2а=8 см, 3а=12 см, 5а=20 см
Стороны треугольника, образованного средними линиями исходного.
8 см, 12 см, 20 см.
---------
Примечание. Именно так решаются подобные задачи. НО! Здесь получается, что большая сторона равна сумме двух других. В решении по данному условию не может быть выполнено правило о неравенстве треугольника, по которому любая сторона треугольника не может быть равна или больше суммы двух других. Вопрос не удален, так как задача с таким же условием давалась другим пользователем и в другое время, значит, составлена с ошибкой.