Предмет: Математика,
автор: unicorn18well
Найти производные функций
Помогите пожалуйста!!
Приложения:
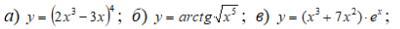
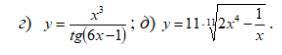
Ответы
Автор ответа:
1
Ответ:
a)
б)
в)
г)
д)
Похожие вопросы
Предмет: Биология,
автор: Armagend
Предмет: Математика,
автор: nastyalobakina
Предмет: Математика,
автор: madikon2004
Предмет: Математика,
автор: Kristinka20061