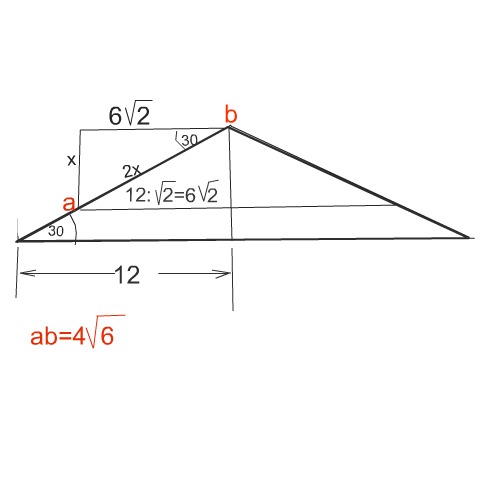
Основание равнобедренного треугольника имеет длину 24. Прямая, параллельная основанию, делит площадь треугольника пополам. Найдите длину отрезка, который эта прямая отсекает от боковой стороны (считая от вершины), если угол при основание составляет 30 градусов.
Ответы
Отношение площадей подобных треугольников равно квадрату коэффициента их подобия.
Так как площади треугольников относятся, как 2:1 (площадь большего к площади меньшего ), то коэффициент подобия - √2
Половина основания большего треугольника равна 24:1=12
Основание меньшего Δ равно
12:√2
Это - дробь 12/√2. Умножив числитель и знаменатель этой дроби на √2, получим длину меньшего основания 6√2
Подрисуем к боковой стороне меньшего треугольника такой же точно до получения прямоугольника с диагональю аb. (Можно не подрисовывать, но так нагляднее в сделанном мной рисунке).
Высота меньшего треугольника лежит против угла 30 °. Следовательно, сторона аb больше этой высоты в 2 раза.
Обозначим высоту х, сторону 2х.
По теореме Пифагора
х²=4х²- (6√2)²
3х²=72
х=√24=2√6
аb=2х=4√6