Предмет: Математика,
автор: JiganLemon
Докажите, что выражение 9x2+8y-6xy+y2+18-24x принимает положительные значения при любых значениях переменных x и y.
Я применил группировку 9x2+8y-6xy+y2+18-24x=9x2-6xy+y2+8y-24x+18=(3x-y)2+8(y-3x)+18 ... Получился квадратный многочлен со смешанной переменной (3x-y).
Можно было бы заменить (3x-y) на t и решить уравнение через дискриминант или построить параболу, но НУЖНО аналитически показать, что выражение положительно при всех значениях x и y (для ученика 7-го класса эти темы еще не доступны).
Помогите, пожалуйста, решить.
Вид многочлена из учебника - во вложении.
Приложения:
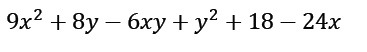
Ответы
Автор ответа:
0
Для начала приравнять к какой-нибудь величине, например А
Нужно сгруппировать 9х2 -6ху и у2
9х2 - 6ху + у2 = (3х - у) ^2 (скобка в квадрате)
В результате получится
(3х - у) ^2 + 8у + 18 - 24х = А
(3х - у) ^2 = А - 8у - 18 + 24х
(3х - у) ^2 = А - (8у + 18 - 24х)
Левая часть уравнения при любых обстоятельствах есть величина положительная, т.к. степень 2 (любая степень с четным значением), следовательно правая часть тоже будет величина положительная
Похожие вопросы
Предмет: Математика,
автор: polina784597
Предмет: Английский язык,
автор: faridamirzaeva86
Предмет: Алгебра,
автор: ppat5547
Предмет: Математика,
автор: Аноним