Предмет: Геометрия,
автор: Darya0903
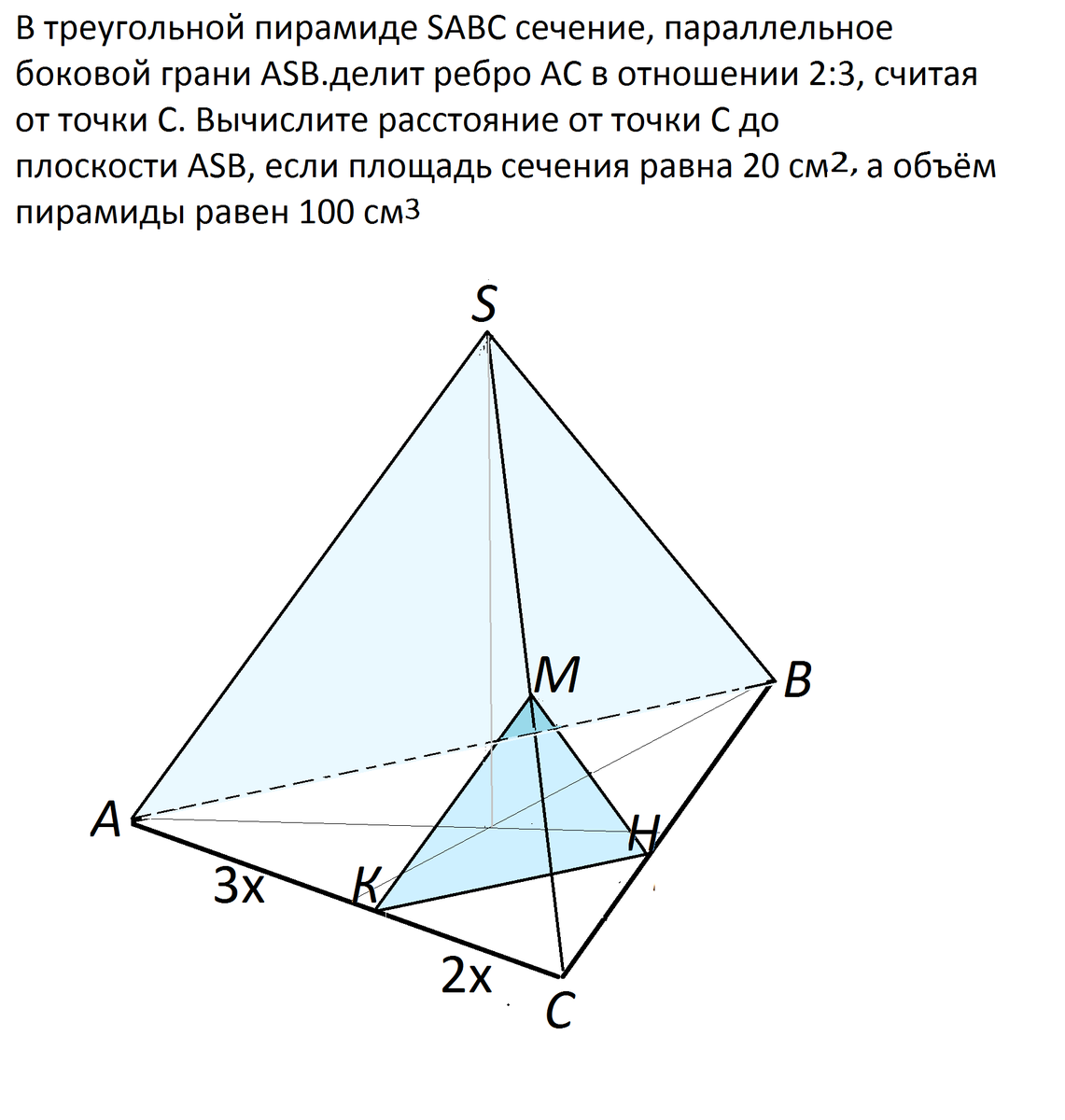
В треугольной пирамиде SABC сечение, параллельное боковой грани ASB.делит ребро АС в отношении 2:3, считая от точки С. Вычислите расстояние от точки С до плоскости ASB, если площадь сечения равна 20 см2, а объём пирамиды равен 100 см3
Ответы
Автор ответа:
0
Представим, что мы повернули эту пирамиду на грань АSD как на основание). Тогда очевидно, что расстояние (перпендикуляр) от С до плоскости этой грани - высота получившейся пирамиды.
КМ параллельна АS. ⇒треугольники АSС и КМС подобны с коэффициентом подобия (3+2):2=2,5
Тогда и треугольники АSB и КМН параллельны и подобны, а коэффициент их подобия тоже 2,5
Площади подобных фигур относятся как квадрат коэффициента их подобия.
S (АSB): S(КМН)=(АС:КС)²=6,25
S (АSB)=S(КМН)*6,25=125 см²
V=hS:3
h=3V:S=300:125=2,4 см
Ответ: расстояние от С до плоскости грани АSB=2,4 см
Приложения:
Похожие вопросы
Предмет: Геометрия,
автор: BLACK1010
Предмет: Биология,
автор: egortropin57
Предмет: Информатика,
автор: polina25816
Предмет: Химия,
автор: pati2014
Предмет: Математика,
автор: Софкаааа