Предмет: Геометрия,
автор: lalalalala96
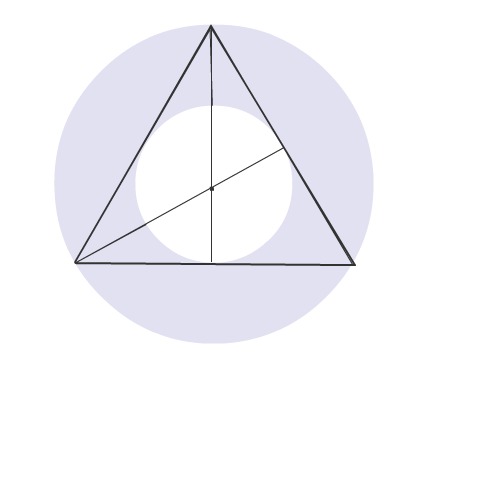
докажите что центры вписанной в равносторонний треугольник окружности и описанной около него совпадают а их радиусы относятся как 2:1....спасибо заранее
Ответы
Автор ответа:
0
Центром описанной вокруг треугольника окружности является точка пересечения срединных перпендикуляров. Центром вписанной в треугольник окружности является точка пересечения биссектрис.
В равностороннем треугольнике эти точки совпадают. А так как высоты ( срединные перпендикуляры) такого треугольника в то же время и его биссектрисы и медианы, а медианы треугольника точкой пересечения делятся в отошении 2:1, то и радиусы данных окружностей имеют такое же отошение.
Приложения:
Похожие вопросы
Предмет: Литература,
автор: oxroeva
Предмет: Английский язык,
автор: Аноним
Предмет: Геометрия,
автор: Sofa000001
Предмет: Математика,
автор: Tory8