Предмет: Алгебра,
автор: ramazanovaalena
Помогите с решением. Пожалуйста
Приложения:
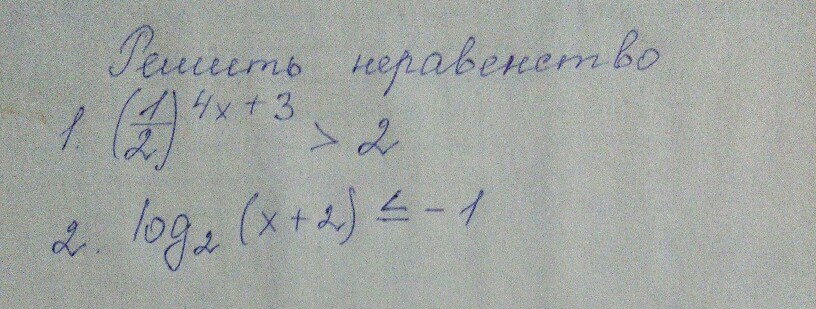
Ответы
Автор ответа:
0
Воспользуемся свойством степеней
Так как 2>1, то функция возрастающая, ЗНАК НЕРАВЕНСТВА НЕ МЕНЯЕТСЯ!!!!!!!
Ответ:
Отметим ОДЗ
Воспользуемся свойством логарифмов
С учетом ОДЗ ответ будет
Похожие вопросы
Предмет: Математика,
автор: askarmagadiev
Предмет: Русский язык,
автор: Korgi13579
Предмет: Математика,
автор: kotmogilkin
Предмет: Биология,
автор: чоколадка23