Предмет: Алгебра,
автор: ollk
ПриветРешите, пожалуйста, уравнения а), в) и в), г)
Очень надо, тема: "Решение уравнений с помощью разложения на множители"
Приложения:
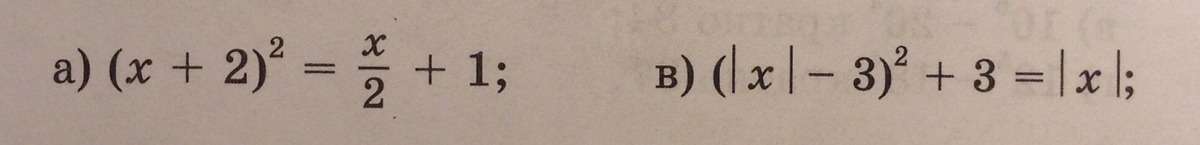
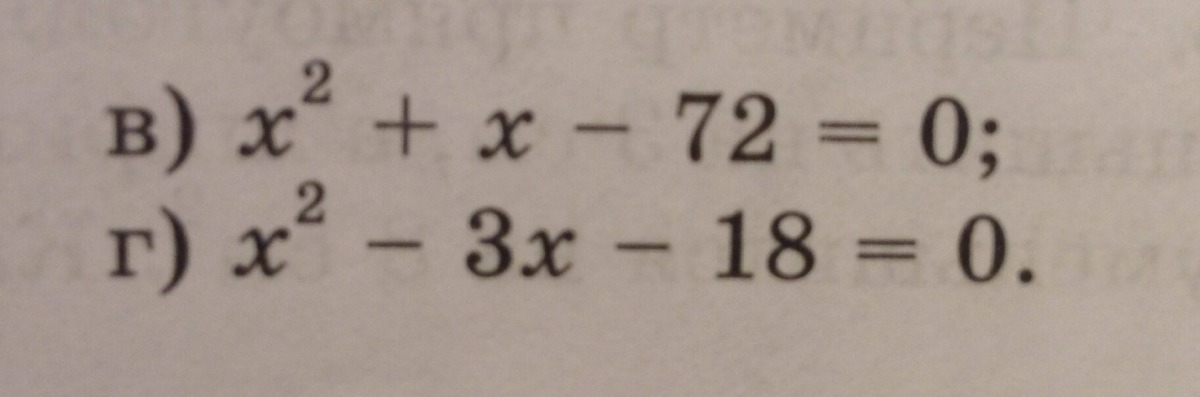
Ответы
Автор ответа:
0
1) (x+2)^2=x/2+1⇒(2(x/2+1))^2=x/2+1⇒4(x/2+1)^2-(x/2+1)=0
x/2+1=t⇒4t^2-t=0⇒t(4t-1)=0⇒t1=0
4t-1=0⇒4t=1⇒t=1/4
a) t=0⇒x/2+1=0⇒x/2=-1⇒x1=-2
b) t=1/4⇒x/2+1=1/4⇒2x+4=1⇒2x=-3⇒x2=-3/2
2) (IxI-3)^2+3=IxI⇒(IxI-3)^2=IxI-3⇒(IxI-3)^2-(IxI-3)=0⇒
IxI-3=t⇒t^2-t=0⇒t(t-1)=0⇒t1=0; t2=1
a) t=0⇒IxI-3=0⇒IxI=3⇒x1=3; x2=-3
b) t=1⇒IxI-3=1⇒IxI=4⇒x3=4; x4=-4
3)x^2+x-72=0
По теореме Виетта
x1+x2=-1; x1*x2=-72⇒
x1=-9; x2=8
4) x^2-3x-18=0
По теореме Виетта
x1+x2=3; x1*x2=-18⇒
x1=6; x2=-3
x/2+1=t⇒4t^2-t=0⇒t(4t-1)=0⇒t1=0
4t-1=0⇒4t=1⇒t=1/4
a) t=0⇒x/2+1=0⇒x/2=-1⇒x1=-2
b) t=1/4⇒x/2+1=1/4⇒2x+4=1⇒2x=-3⇒x2=-3/2
2) (IxI-3)^2+3=IxI⇒(IxI-3)^2=IxI-3⇒(IxI-3)^2-(IxI-3)=0⇒
IxI-3=t⇒t^2-t=0⇒t(t-1)=0⇒t1=0; t2=1
a) t=0⇒IxI-3=0⇒IxI=3⇒x1=3; x2=-3
b) t=1⇒IxI-3=1⇒IxI=4⇒x3=4; x4=-4
3)x^2+x-72=0
По теореме Виетта
x1+x2=-1; x1*x2=-72⇒
x1=-9; x2=8
4) x^2-3x-18=0
По теореме Виетта
x1+x2=3; x1*x2=-18⇒
x1=6; x2=-3
Похожие вопросы
Предмет: Химия,
автор: linaidahar
Предмет: Русский язык,
автор: dhsthjhgsdysr
Предмет: Литература,
автор: ananas098657
Предмет: Математика,
автор: boboshko1983
Предмет: Геометрия,
автор: natalitalakova