Предмет: Алгебра,
автор: Аноним
нужно решить два уравнения, подробно(см вложения)
Приложения:
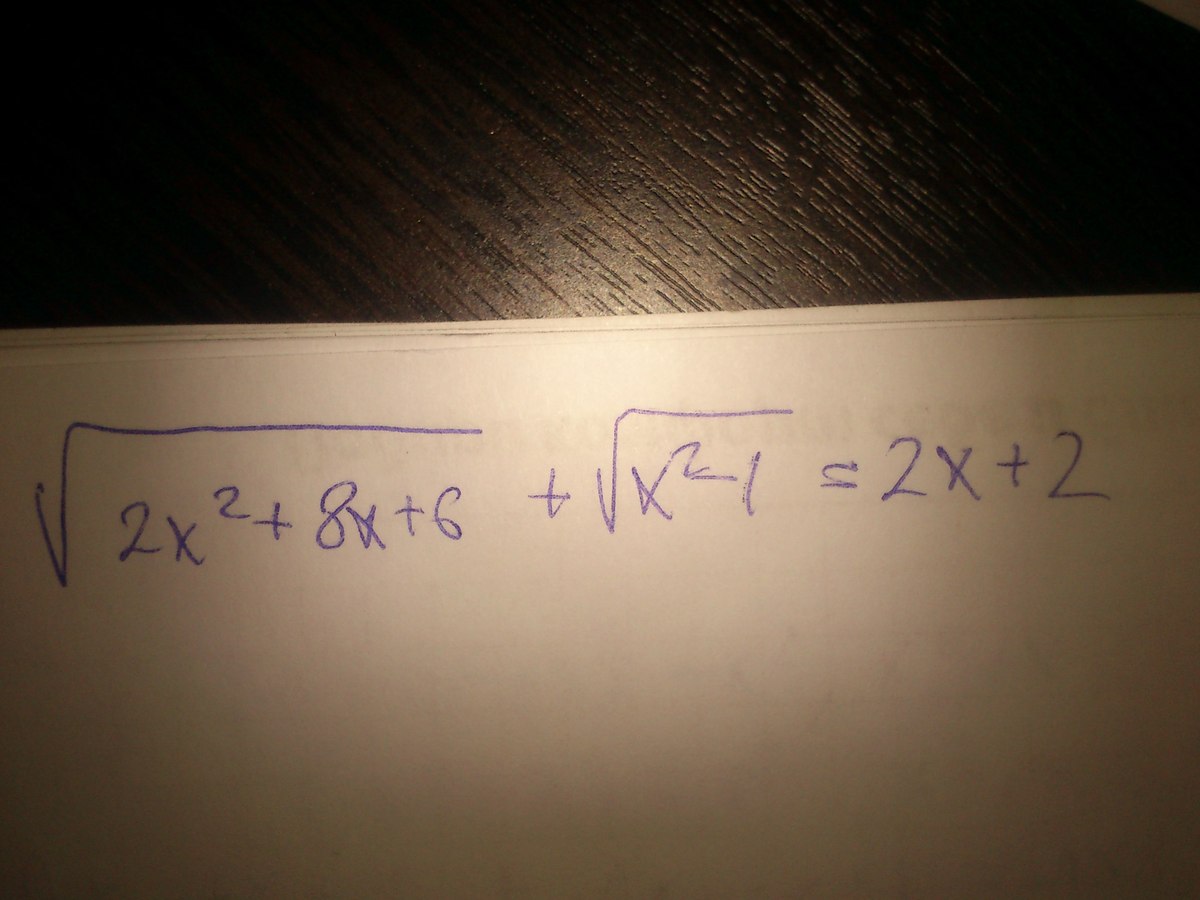
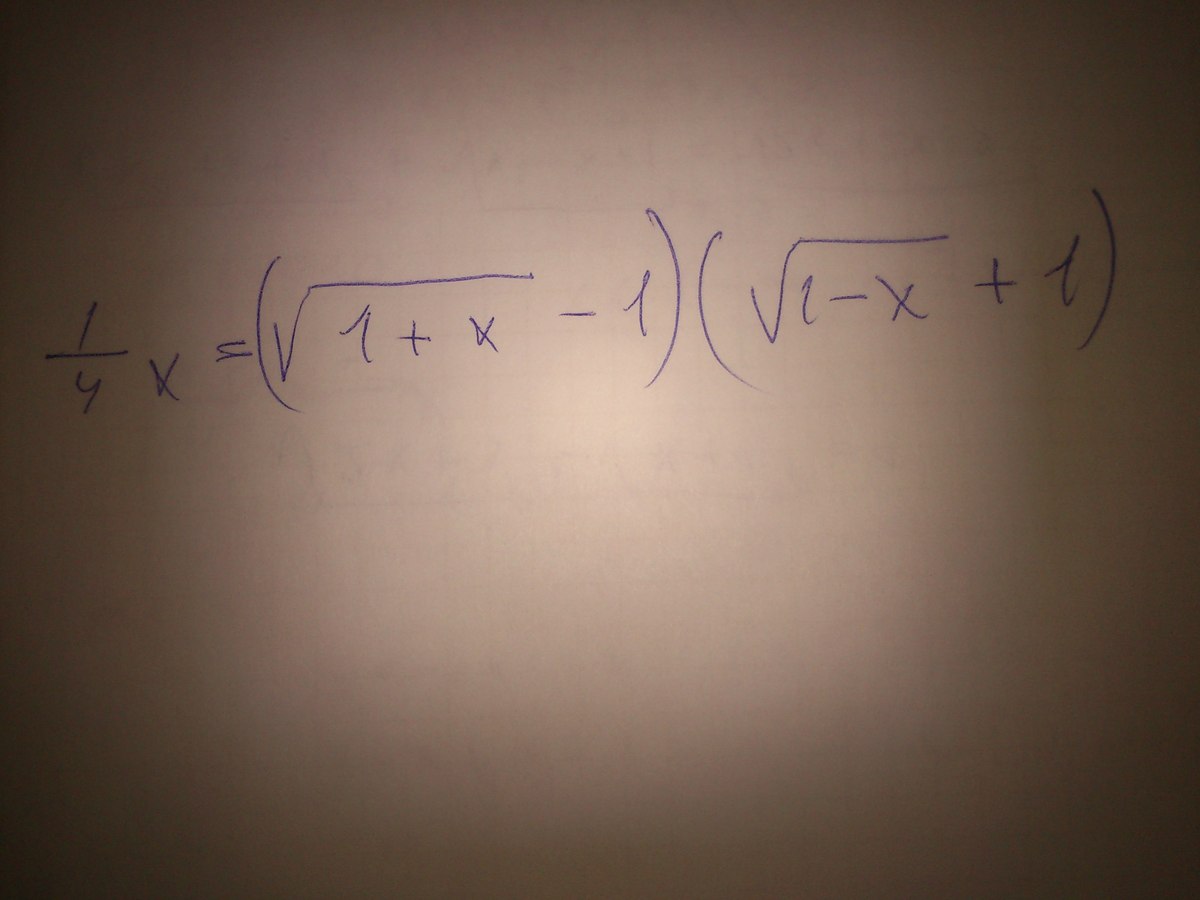
Ответы
Автор ответа:
0
Первый скрин решил. А второй уже лень. Если ещё надо, то напиши.
Приложения:

Автор ответа:
0
ответ: -1; 1
ответ: 0
Приложения:

Похожие вопросы
Предмет: Геометрия,
автор: abujnova0
Предмет: Английский язык,
автор: tulegenakmerej
Предмет: Геометрия,
автор: Itskatyamar
Предмет: Математика,
автор: valerik0716
Предмет: Алгебра,
автор: Аноним