Question

найти везде периметр...

Answer 1

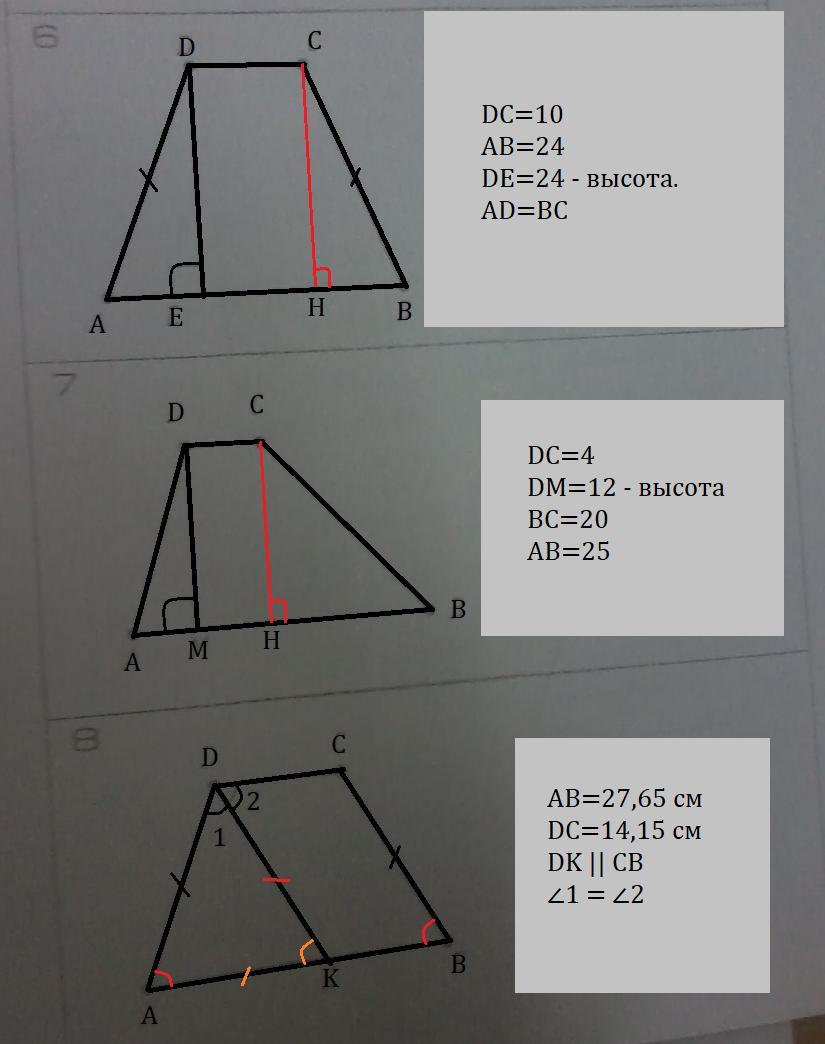
6.

Проведём СН перпендикулярную АВ. Получается, что DC=EH=10.

AE=HB (т.к. трапеция рб)

AE+HB=AB-EH=24-10=14

т.к. AE=HB, то AE=7, HB=7

По теореме Пифагора находим AD

$AD=sqrt{24^2+7^2}=sqrt{576+49}=25$

Периметр трапеции=AD+DC+AB+CB=25+10+24+25=84

7.

Проведём СН перпендикулярную АВ. DM=CH=12

Найдём по т.Пифагора HB.

$HB=sqrt{20^2-12^2}=sqrt{400-144}=16$

Отсюда, АМ=АВ-НВ=25-16=9

Находим по т.Пифагора AD

$AD=sqrt{12^2+9^2}=sqrt{144+81}=15$

Периметр трапеции=15+4+25+20=64

8.

угол AKD=углу KDC

угол AKD=углу ABC

угол DAB=углу ABC (т.к. трапеция рб)

Из этого следует, что треугольник ADK - равносторонний.

AK=AB-KB

KB=DC=14,15

AK=27,65-14,15=13,5

AD=BC=13,5

Периметр = 14,15+27,65+2*13,5=68,8

Answer 2

6.

H∈AB; CH⊥AB (по построению) и DE⊥AB (по условию) ⇒ CH║DE; CH=DE - как отрезки заключённые между параллельными прямыми и лежащие на параллельных прямых. Значит DCHE - прямоугольник ⇒ DC=EH=10

ΔADE=ΔBCH по гипотенузе и катету ⇒ AE=HB ⇒ AE=(AB-EH):2=(24-10):2=7.

$AD=sqrt{DE^2+AE^2}=sqrt{24^2+7^2}=sqrt{576+49}=25$

Как гипотенуза ΔADE. AD=BC=25

P(ABCD)=AB+BC+CD+DA=24+25+10+25=50+34=84.

Ответ: 84.

7.

H∈AB; CH⊥AB (по построению) и DM⊥AB (по условию) ⇒ CH║DM; CH=DM=12 - как отрезки заключённые между параллельными прямыми и лежащие на параллельных прямых. Значит DCHM - прямоугольник ⇒ DC=MH=4

$HB=sqrt{BC^2-CH^2}=sqrt{20^2-12^2}=\sqrt{8cdot 32}=sqrt{2^3cdot 2^5}=2^4=16$

Как катет прямоугольного ΔCHB. AM=AB-MH-HB=25-16-4=5

$AD=sqrt{AM^2+DM^2}=sqrt{5^2+12^2}=13$

Как гипотенуза ΔDMH.

P(ABCD)=AB+BC+CD+DA=25+20+4+13=45+17=62

Ответ: 62.

8.

DC║KB - как отрезки лежащие на основании трапеции.

DK║CB - по условию, поэтому DCBK - параллелограмм, значит DK=CB и ∠KBC=∠KDC=∠2; ∠AKD=∠KBC - как соответственные.

∠DAB=∠ABC - как углы при основании трапеции. В итоге в ΔADK все 3 угла равны, значит он равносторонний.

KB=DC=14,15 см как противоположные стороны параллелограмма.

AK=AB-KB=27,65см - 14,15 см=13,5 см. AD=AK=13,5 см - как стороны равностороннего треугольника. AD=BC - по условию.

P(ABCD) = AB+BC+CD+DA = 27,65см+13,5см+14,15см+13,5см = 41,8см+27см = 68,8см

Ответ: 68,8см.