Предмет: Алгебра,
автор: marinka31
Определить четность или нечетность функции
Приложения:
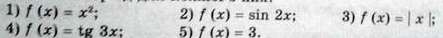
Ответы
Автор ответа:
0
Автор ответа:
0
f(x) = 3
Подразумевается, что
Подразумевается, что
Автор ответа:
0
Нет, мы взяли -x и подставили в модуль, на выходе мы получили ответ равный начальному. Следовательно, функция чётная
Автор ответа:
0
Линейная функция задаётся формулой f(x) = kx + b.В нашем случае k = 0. Стандартная формула будет записана так: f(x) = 0x + 3. Подставив любое значение x мы получим 0 × x = 0. Следовательно, функция не зависит от значений x.
Автор ответа:
0
спасибо)))
Автор ответа:
0
Всегда пожалуйста.
Похожие вопросы
Предмет: Другие предметы,
автор: Аноним
Предмет: Физика,
автор: mariiaKa
Предмет: Физика,
автор: mariiaKa
Предмет: Физика,
автор: Kolbasohka