Предмет: Алгебра,
автор: marwuga
Помогите решить систему уравнений:
Приложения:
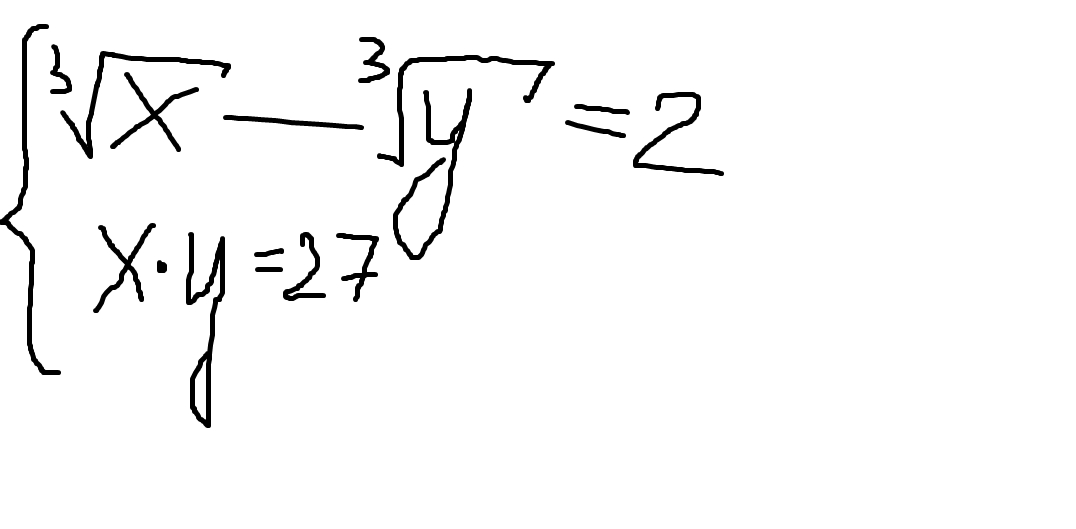
Ответы
Автор ответа:
0
∛x - ∛y = 2
xy = 27
y = 27/x
∛x - ∛(27/x) = 2
y = 27/x
∛x - 3∛(1/x) = 2 / *(∛x)
(∛x)² - 2(∛x) - 3 = 0
∛x = z
z² - 2z - 3 = 0
z₁ = - 1
z₂ = 3
∛x = - 1
x₁ = - 1
∛x = 3
x₂ = (3)³
x₂ = 27
y₁ = 27/(-1)
y₁ = - 27
y₂ = 27/27
y₂ = 1
Ответ: (- 1; - 27) (27;1)
xy = 27
y = 27/x
∛x - ∛(27/x) = 2
y = 27/x
∛x - 3∛(1/x) = 2 / *(∛x)
(∛x)² - 2(∛x) - 3 = 0
∛x = z
z² - 2z - 3 = 0
z₁ = - 1
z₂ = 3
∛x = - 1
x₁ = - 1
∛x = 3
x₂ = (3)³
x₂ = 27
y₁ = 27/(-1)
y₁ = - 27
y₂ = 27/27
y₂ = 1
Ответ: (- 1; - 27) (27;1)
Похожие вопросы
Предмет: Английский язык,
автор: abbasqurbanli439
Предмет: Русский язык,
автор: HAPLUNA
Предмет: Другие предметы,
автор: 1709200213179
Предмет: Физика,
автор: slk1919
Предмет: Математика,
автор: Аноним