Предмет: Алгебра,
автор: Florida777
ПОМОГИТЕ,ПОЖАЛУЙСТА,40 БАЛЛОВ!
Приложения:
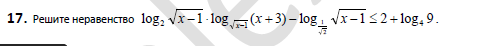
Ответы
Автор ответа:
0
Рассмотрим функцию
Найдем область определения:
2. Приравняем функцию к нулю
Воспользуемся формулами перехода к новому основанию
Воспользуемся свойством монотонности логарифмической функции
По т. Виета
Полученное решение отметим на промежутке
-(1)___-___(2)___-___[3]____+____>
Ответ:
Автор ответа:
0
Еще в ответе от 1 до 2 не включая
Автор ответа:
0
Ай точно
Автор ответа:
0
Решение изменил
Автор ответа:
0
ок,спасибо большое)
Автор ответа:
0
http://znanija.com/task/9757395 не решите?
Автор ответа:
0
---------------------------------------------------
Приложения:
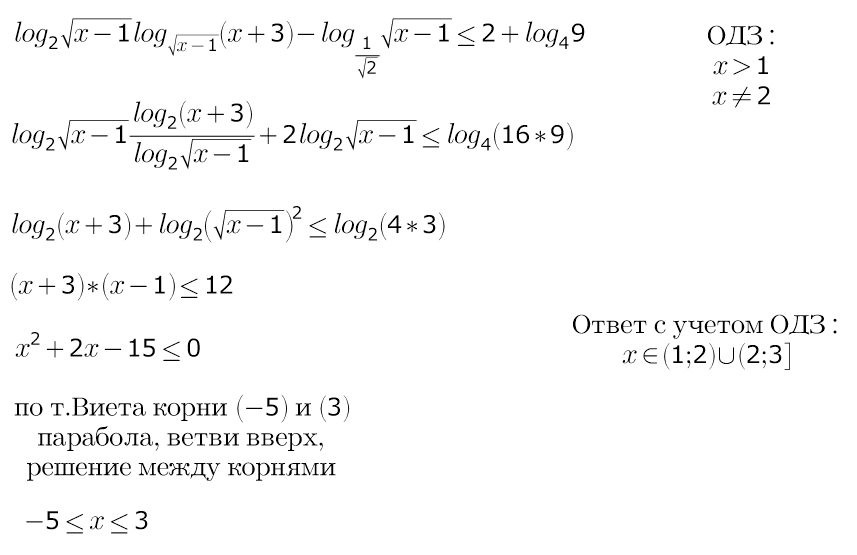
Похожие вопросы
Предмет: Геометрия,
автор: armanasia0710
Предмет: Окружающий мир,
автор: Аноним
Предмет: Химия,
автор: karaevafotikmailcom
Предмет: Химия,
автор: 555Д
Предмет: Математика,
автор: shirvanova73