Question

задача на произвольный треугольник !

известны стороны  a=10 , b=9,c=17 произвольного  треугольника

1)Определите косинус большего угла2) Определите вид треугольника 3)Начертите чертеж , соответствующий виду треугольника 4)Вычислите а)периметр треугольника б)площадь треугольника в)высоту , проведенную к стороне а г)радиус окружности , вписанной в данный треугольник д) радиус  окружности , описанной около треугольника . 

Answer 1

1) Наибольший угол лежит против наибольшей стороны.

По теореме косинусов

$cos C=frac{a^2+b^2-c^2}{2ab}=frac{10^2+9^2-17^2}{2*10*9}=-0.6$

2) так как косинус наибольшего угла cos C=-0.6<0, то угол С - тупой, а треугольник тупоугольный

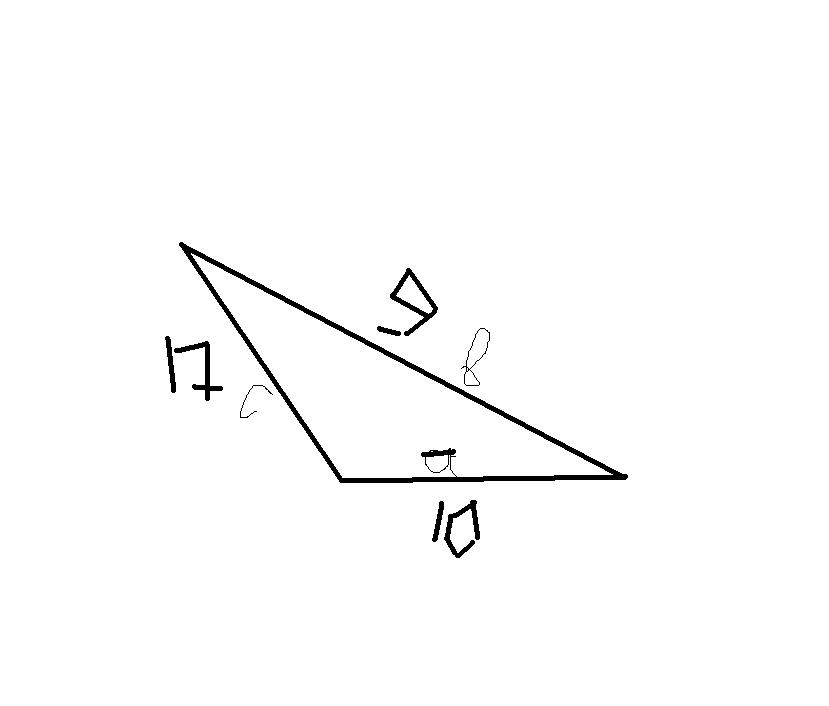
3) см.вложение

4) а) Р=a+b+c=10+9+17=36

б) полупериметр равен p=P/2=36/2=18

площадь треугольника по формуле Герона равна

$S=sqrt{p(p-a)(p-b)(p-c)}=sqrt{18*(18-10)*(18-9)*(18-17)}=18sqrt{5}$

в)высота, проведенная к стороне а равна

$h_a=frac{2S}{a}=frac{2*18sqrt{5}}{10}=3.6sqrt{5}$

г) радиус окружности, вписанный в данный треугольник равен

$r=frac{S}{p}=frac{18sqrt{5}}{18}=sqrt{5}$

д) радиус окружности, описанной около треугольника равен

$R=frac{abc}{4S}=frac{10*9*17}{4*18sqrt{5}}=4.25sqrt{5}$