Question

!!19 б+10 за лучший!! Найти площадь ромба, меньшая диагональ которого равна √3, а острый угол равен 60°. В ответе указать S√3. Пожалуйста распишите чтобы понятно было :3

Answer 1

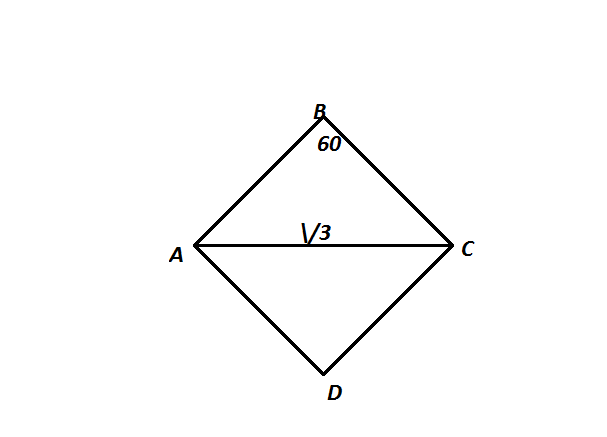
Назовем ромб ABCD и рассмотрим треугольник ABC. (рис1)
Т.к. все стороны ромба равны, AB=BC, треугольник является равнобедренным, а т.к. угол abc=60°, треугольник также будет равносторонним, след-но AB=BC=AC=√3.
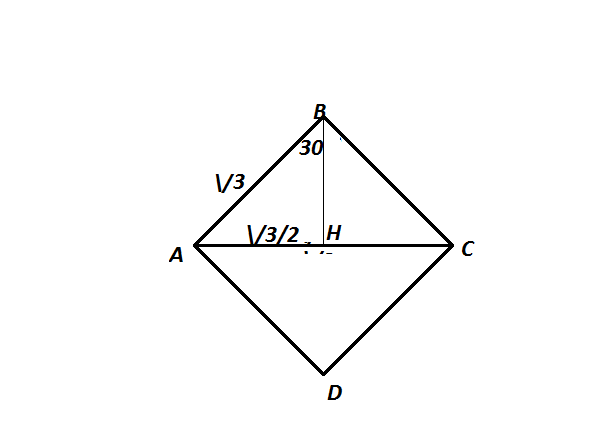
Проведем в этом треугольнике высоту BH.(рис 2) Согласно свойствам равностороннего треугольника, она также является медианой и биссектрисой.
Рассмотрим треугольник ABH. В нем гипотенуза AB=√3, а катетAH=(√3)/2. Найдем катет BH. 
cos(abh)=BH/AB. BH=AB·cos(abh)=√3*√3/2=3/2. И это половина диагонали BD.
Тогда BD=2·BH=3;
Найдем площадь ромба, как половину произведения диагоналей $S= frac{1}{2} BD*AC= frac{1}{2}*3* sqrt{3} =frac{3 sqrt{3} }{2}$
Тогда $S sqrt{3} = frac{3 sqrt{3} }{2}* sqrt{3} = frac{3*3}{2} = frac{9}{2} =4.5$