Предмет: Геометрия,
автор: Ярославааа
Помогите решить пожалуйста !!!!!!
В треугольнике ABC, AC=20 см ,угол A равен 30 ,угол C равен 105 .Найдите длину стороны BC.
Ответы
Автор ответа:
0
угол B=180-30-105=45
Проведем в треугольнике высоту CH (рис 1)
Рассмотрим треугольник AHC (рис 2)

Рассмотрим треугольник BHC (рис 3)
т.к. B=45град, то и угол C здесь буде равен 45 => треугольник равнобедренный, CH=HB=10;
Тогда
Проведем в треугольнике высоту CH (рис 1)
Рассмотрим треугольник AHC (рис 2)
Рассмотрим треугольник BHC (рис 3)
т.к. B=45град, то и угол C здесь буде равен 45 => треугольник равнобедренный, CH=HB=10;
Тогда
Приложения:

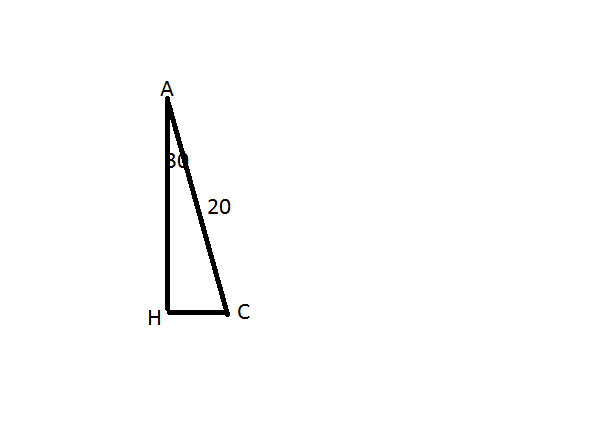

Автор ответа:
0
спасибо большое :)
Автор ответа:
0
не за что ^^
Автор ответа:
0
В треугольнике известны все углы( 30, 105,45) и одна сторона. Чтобы найти любую сторону, надо использовать т. синусов.
ВС/Sin 30 = AC/Sin 45
ВС/ 1/2 = 20/ √2/2
ВС= 20·1/2·2/√2= 20√2/2 = 10√2
ВС/Sin 30 = AC/Sin 45
ВС/ 1/2 = 20/ √2/2
ВС= 20·1/2·2/√2= 20√2/2 = 10√2
Приложения:

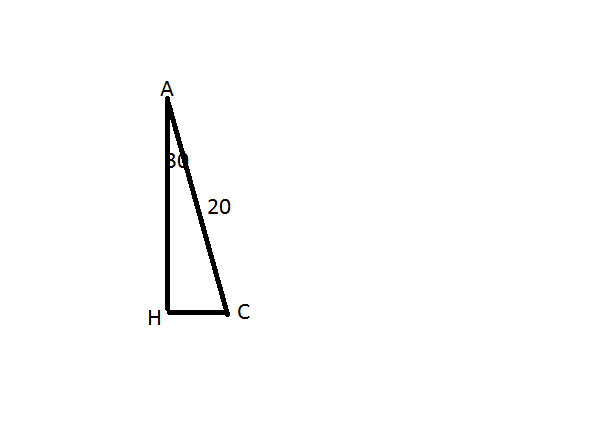

Похожие вопросы
Предмет: Українська мова,
автор: sanysmirnov697
Предмет: Английский язык,
автор: vladimirromanov1996
Предмет: История,
автор: whatapity
Предмет: Геометрия,
автор: CaбиНОЧКА
Предмет: Литература,
автор: asarin1664