Предмет: Алгебра,
автор: Dashidze97
Решите систему уравнения
Приложения:
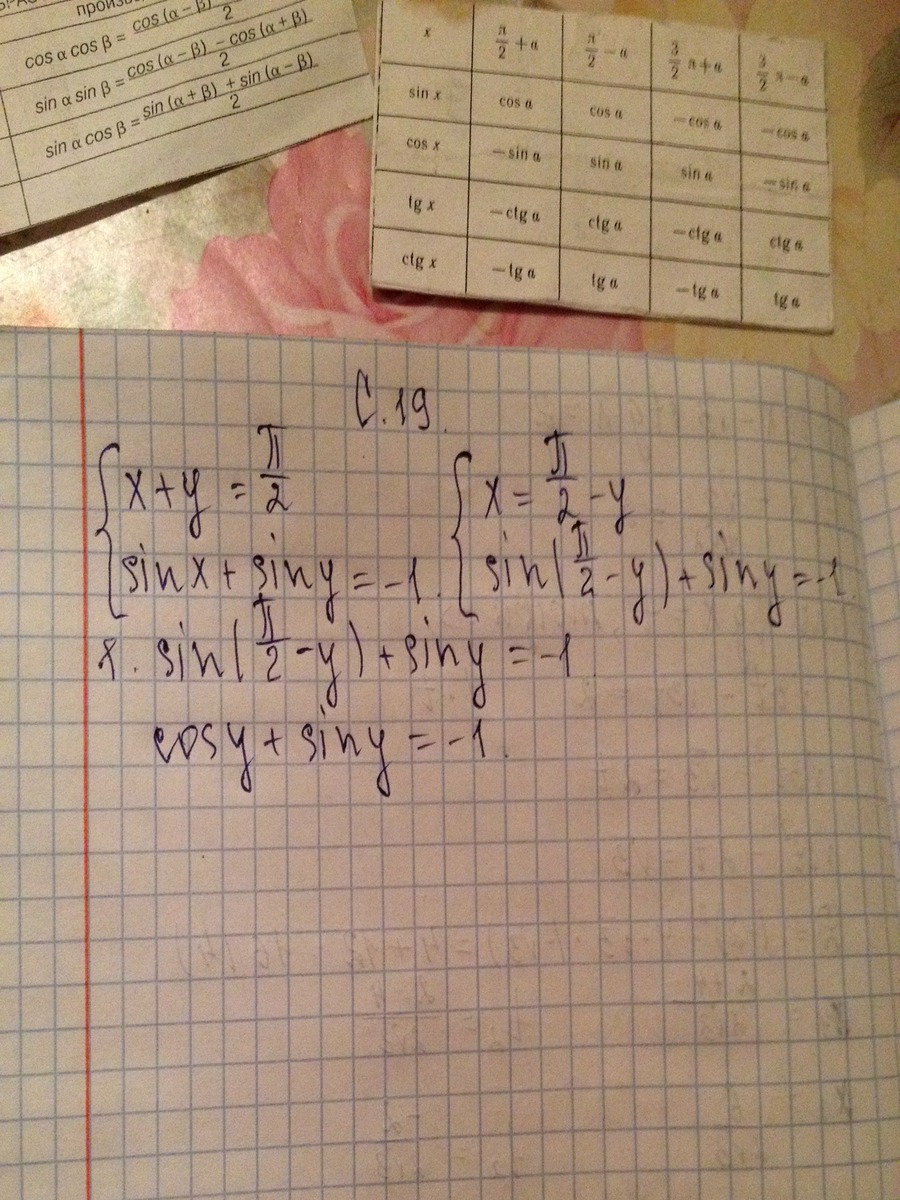
Ответы
Автор ответа:
0
Начали решать верно, продолжу.
Перейдем к половинному углу:



Подставим в уравнение и упростим:



1)


2)




Найдем теперь х:
1)

2)

Перейдем к половинному углу:
Подставим в уравнение и упростим:
1)
2)
Найдем теперь х:
1)
2)
Автор ответа:
0
Это продолжение после моего решения?
Автор ответа:
0
да, я же написала выше
Автор ответа:
0
Спасибо
Похожие вопросы
Предмет: Геометрия,
автор: marsardv
Предмет: Математика,
автор: Аноним
Предмет: Информатика,
автор: Аноним
Предмет: История,
автор: msk220208
Предмет: Химия,
автор: zyklop97